题目内容
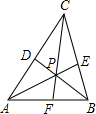
通过学习我们已经知道三角形的三条内角平分线是交于一点的．如图，P是△ABC的内角平分线的交点，已知P点到AB边的距离为1，△ABC的周长为10，则△ABC的面积为________．
5
分析：由于P是△ABC的内角平分线的交点，所以根据角平分线的性质在知道P到三边的距离相等，而S△ABC=S△APC+S△APB+S△BPC，并且S△APC=
×1×AC，依次就可以表示其他三角形的面积，然后利用△ABC的周长即可求出S△ABC的值．
解答：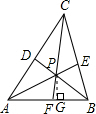
解：∵P是△ABC的内角平分线的交点，
∴P到三边的距离相等，即到三边的距离都是1，
∴S△ABC=S△APC+S△APB+S△BPC=×1×AC+×1×BC+×1×AB
=×1×（AC+BC+AB）
=×1×10=5．
所以△ABC的面积是5．
故填空答案：5．
点评：本题考查了角平分线的性质；题目主要利用了三角形的三条角平分线交于一点，并且这一点到三角形三边的距离相等来求三角形的面积，在计算时采用了面积的割补法，没有直接利用公式去求．
分析：由于P是△ABC的内角平分线的交点，所以根据角平分线的性质在知道P到三边的距离相等，而S△ABC=S△APC+S△APB+S△BPC，并且S△APC=
×1×AC，依次就可以表示其他三角形的面积，然后利用△ABC的周长即可求出S△ABC的值．解答：
解：∵P是△ABC的内角平分线的交点，∴P到三边的距离相等，即到三边的距离都是1，
∴S△ABC=S△APC+S△APB+S△BPC=
×1×AC+×1×BC+×1×AB=
×1×（AC+BC+AB）=
×1×10=5．所以△ABC的面积是5．
故填空答案：5．
点评：本题考查了角平分线的性质；题目主要利用了三角形的三条角平分线交于一点，并且这一点到三角形三边的距离相等来求三角形的面积，在计算时采用了面积的割补法，没有直接利用公式去求．
练习册系列答案
阅读快车系列答案
相关题目
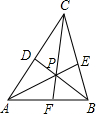通过学习我们已经知道三角形的三条内角平分线是交于一点的．如图，P是△ABC的内角平分线的交点，已知P点到AB边的距离为1，△ABC的周长为10，则△ABC的面积为
（2014•宝山区一模）通过锐角三角比的学习，我们已经知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长比与角的大小之间可以相互转化．类似的我们可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图在△ABC中，AB=AC，
