题目内容
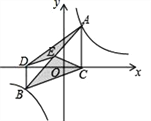
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,D是AB上的一点
,D是AB上的一点![]() 不与点A,B重合
不与点A,B重合![]() ,连接CD,以点C为中心,把CD顺时针旋转
,连接CD,以点C为中心,把CD顺时针旋转![]() ,得到CE,连接AE.
,得到CE,连接AE.
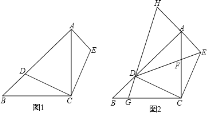
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,若
如图2,若![]() ,点G为BC上一点,连接GD并延长,与EA的延长线交于点H,且
,点G为BC上一点,连接GD并延长,与EA的延长线交于点H,且![]() ,连接DE与AC相交于点F,请写出图2中所有正切值为2的角.
,连接DE与AC相交于点F,请写出图2中所有正切值为2的角.
【答案】(1)证明见解析;(2)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由已知可知∠B=∠CAB=45°,由旋转可证△BCD≌△ACE,由全等三角形的性质可得∠CAE=∠B=45°,从而得∠EAD=90°;
(2)取DE的中点O,连接AO,CO,作DN⊥BC于N,GM⊥BD于M,可知A、D、C、E四点共圆,得到∠AED=∠ACD,由tan∠AED=![]() 和AE=BD,AD=2BD,即可得到∠AED和∠ACD的正切值为2;由tan∠HGC=3得到DN=3GN,设GN=a,则DN=BN=3a,BG=2a,BD=
和AE=BD,AD=2BD,即可得到∠AED和∠ACD的正切值为2;由tan∠HGC=3得到DN=3GN,设GN=a,则DN=BN=3a,BG=2a,BD= ![]() a,BM=GM=
a,BM=GM=![]() a,从而tan∠DGM=∠H=2.
a,从而tan∠DGM=∠H=2.
![]() 证明:如图1中,
证明:如图1中,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
![]() 解:如图2中,取DE的中点O,连接AO,CO,作
解:如图2中,取DE的中点O,连接AO,CO,作![]() 于H,
于H,![]() 于M.
于M.

![]() ,
,![]() ,
,
![]() ,
,
![]() ,D,C,E四点共圆,
,D,C,E四点共圆,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 满足条件的角有
满足条件的角有![]() ,
,![]() ,
,![]() .
.
故答案为:(1)证明见解析;(2)∠AED,∠ACD,∠H.

【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个,某学习小组进行摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再放回,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
![]() 当n很大时,估计从袋中摸出一个黑球的概率是______;
当n很大时,估计从袋中摸出一个黑球的概率是______;
![]() 试估算口袋中白球有______个;
试估算口袋中白球有______个;
![]() 在
在![]() 的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.
的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.