题目内容
若等腰三角形的一个内角是另一个内角的2倍，则满足条件的形状不同的三角形有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析：设等腰三角形的三个内角的大小分别为a、b、b，则a+2b=π，若a=2b，代入求出a b；若b=2a，代入求出a b；即可得出答案．
解答：设等腰三角形的三个内角的大小分别为a、b、b，则a+2b=180°，
若a=2b，解之得a=90°，b=45°；
若b=2a，解之得a=36°，b=72°，
所以满足条件的形状不同的三角形只有2个，
故选B．
点评：本题考查了对等腰三角形的性质和三角形的内角和定理的应用，关键是求出所有情况：①a=2b，②b=2a（a b分别是等腰三角形的顶角和底角）．
分析：设等腰三角形的三个内角的大小分别为a、b、b，则a+2b=π，若a=2b，代入求出a b；若b=2a，代入求出a b；即可得出答案．
解答：设等腰三角形的三个内角的大小分别为a、b、b，则a+2b=180°，
若a=2b，解之得a=90°，b=45°；
若b=2a，解之得a=36°，b=72°，
所以满足条件的形状不同的三角形只有2个，
故选B．
点评：本题考查了对等腰三角形的性质和三角形的内角和定理的应用，关键是求出所有情况：①a=2b，②b=2a（a b分别是等腰三角形的顶角和底角）．
练习册系列答案
寒假学与练系列答案
相关题目
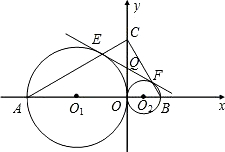在x轴上是否存在点P，使得△PMN是一个以MN为一直角边的等腰直角三角形？若存在，求出P点坐标；若不存在，请说明理由．
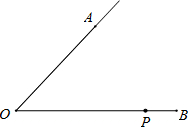（1）如图，已知∠AOB=40°，P为OB上的一点，在∠AOB内，求作一个以OP为底边，底角为20°的等腰三角形OCP（尺规作图，要求保留作图痕迹，不必写出作法）．
已知一次函数y=2x-1和反比例函数y=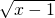
在实数范围内有意义，则x的取值范围是x＞1；