题目内容
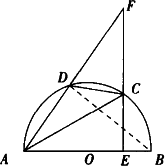
 如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于点D,E若△CDE的面积与四边形ABED的面积相等,则∠C等于
如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于点D,E若△CDE的面积与四边形ABED的面积相等,则∠C等于
- A.30°
- B.40°
- C.45°
- D.60°
C
分析:由已知可得到△ABC的面积是△CDE的面积的2倍,根据相似三角形的判定方法从而得到△CDE∽△CDA,根据面积比可求得相似比,从而根据三角函数即可求得∠C的度数.
解答: 解:连接AE.
解:连接AE.
∵AB是直径,
∴∠AEB=90°.
∵△CDE的面积与四边形ABED的面积相等,
∴△ABC的面积是△CDE的面积的2倍.
∵∠CED+∠DEB=180°,∠DEB+∠DAB=180°,
∴∠CED=∠CAB,∠C=∠C,
∴△CDE∽△CBA.
∴S△CDE:S△CBA=CD2:CB2=1:2.
∴cosC=CD:CB= :2.
:2.
∴∠C=45°.
故选C.
点评:本题考查直径对的圆周角是直角,相似三角形的判定和性质,圆内接四边形的性质等知识的综合运用.
分析:由已知可得到△ABC的面积是△CDE的面积的2倍,根据相似三角形的判定方法从而得到△CDE∽△CDA,根据面积比可求得相似比,从而根据三角函数即可求得∠C的度数.
解答:
 解:连接AE.
解:连接AE.∵AB是直径,
∴∠AEB=90°.
∵△CDE的面积与四边形ABED的面积相等,
∴△ABC的面积是△CDE的面积的2倍.
∵∠CED+∠DEB=180°,∠DEB+∠DAB=180°,
∴∠CED=∠CAB,∠C=∠C,
∴△CDE∽△CBA.
∴S△CDE:S△CBA=CD2:CB2=1:2.
∴cosC=CD:CB=
 :2.
:2.∴∠C=45°.
故选C.
点评:本题考查直径对的圆周角是直角,相似三角形的判定和性质,圆内接四边形的性质等知识的综合运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
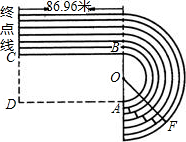 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)