��Ŀ����
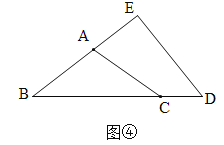
����Ŀ����ͼ���ڵȱߡ�ABC�����߶�AMΪBC���ϵĸ���D��AM�ϵĵ�����CDΪһ������CD���·����ȱߡ�CDE������BE��
��1���������ACB=____����CAM=____��
��2����֤����AOC�ա�BEC��
��3���ӳ�BE������AM�ڵ�F�����ͼ�β��������������BFM�Ķ�����
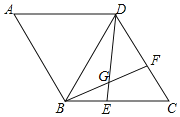
��4��������D������AM��������BC�·�ʱ����ֱ��BE��ֱ��AM�Ľ���ΪF����BFM�Ĵ�С�Ƿ����仯�������������ڱ���ͼ�����ͼ������ֱ��д����BFM�Ķ��������仯����д���仯������

���𰸡���1��60�㣬30�㣻��2���𰸼���������3��60�㣻��4����BFM��60�㣮
�������������������1�����ݵȱ������ε����ʼ��ɽ��н��
��2�����ݵȱ������ε����ʾͿ��Եó�AC=AC��DC=EC����ACB=��DCE=60�����ɵ�ʽ�����ʾͿ��ԡ�BCE=��ACD������SAS�Ϳ��Եó���ADC�ա�BEC��
��3����ȫͼ�Σ�����ADC�ա�BEC�á�CAM=��CBE=30��,���������ڽǺͶ���������á�BFM�Ķ�����
��4��������Ӧͼ�Σ���֪����D���߶�AM���ӳ���������BC�·�ʱ����ͼ�����Եó���ACD�ա�BCE�������õ���CBE=��CAD=30�����ݴ˵ó����ۣ�
���������(1)����ABC�ǵȱ������Σ�
���ACB=60����
���߶�AMΪBC���ϵĸߣ�
���CAM=![]() ��BAC=30����
��BAC=30����
�ʴ�Ϊ��60��30����
��3������ABC����DEC���ǵȱ������Σ�
��AC=BC,CD=CE,��ACB=��DCE=60����
���ACD+��DCB=��DCB+��BCE��
���ACD=��BCE.
����ADC����BEC��
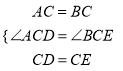 ��
��
����ACD����BCE(SAS)��
��3����ȫͼ�����£�
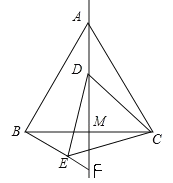
�ɣ�1����2���á�CAM=30������ADC�ա�BEC��
���CBE=��CAM=30����
�ߡ�BMF=90����
���BFM=60����
��4��������D������AM�ϣ�����BC�·�ʱ������ͼ�����£�
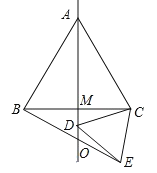
����ABC����DEC���ǵȱ������Σ�
��AC=BC,CD=CE,��ACB=��DCE=60����
���ACB+��DCB=��DCB+��DCE��
���ACD=��BCE��
����ACD����BCE��
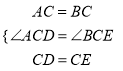 ��
��
����ACD����BCE(SAS)��
���CBE=��CAD=30����
�֡ߡ�AMC=��BMO��
���AOB=��ACB=60��.
������D������AM��ʱ,��AOBΪ��ֵ60��.

 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�