Question

为了美化校园，同学们要在一块正方形空地上种上草，他们设计了图4所示的图案，其中阴影部分为绿化面积，哪个图案的绿化面积与其他图案的绿化面积不相等（　　）

• A、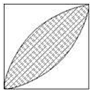
• B、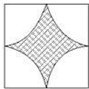
• C、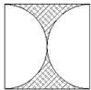
• D、

Answer 1

分析：可以看出B、C、D三个图案中的阴影部分的面积都是正方形的面积和一个以正方形边长为直径的圆的面积的差．但第一个不是，由此可判断出正确的选项．

解答：解：设正方形的边长为a，则有：
S_A=2S_扇形-S_正方形=-a²+

1

2

πa²；
S_B=S_正方形-4S_扇形=a²-4×

90π•a2

360

=a²-πa²；
S_C=S_正方形-2S_扇形=a²-2×

180π•a2

360

=a²-πa²；
S_D=S_正方形-S_圆=a²-πa²；
因此S_B=S_C=S_D，故本题选A．

点评：本题的关键是看出阴影部分的面积是由哪几部分组成的，然后按面积公式计算即可．