题目内容
【题目】如图,在坐标系中,正比例函数y=﹣x的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
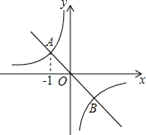
①试根据图象求k的值;
②P为y轴上一点,若以点A、B、P为顶点的三角形是直角三角形,试直接写出满足条件的点P所有可能的坐标.
【答案】①﹣1;②点P的所有可能的坐标是(0,![]() ),(0,﹣
),(0,﹣![]() ),(0,2),(0,﹣2).
),(0,2),(0,﹣2).
【解析】
试题分析:①利用点A在直线y=﹣x上确定A点坐标,然后把A点坐标代入y=![]() 即可求出k的值;
即可求出k的值;
②设P(0,t),而B点坐标为(1,﹣1),分类讨论:当∠PAB=90°,则PA2+AB2=PB2;当∠PBA=90°,则PB2+AB2=PA2;当∠APB=90°,则PA2+PB2=AB2,然后利用两点间的距离公式列出关于t的3个方程,再解方程求出t即可得到P点坐标.
解:①把x=﹣1代入y=﹣x得y=1,
∴A的坐标是(﹣1,1),
把A(﹣1,1)代入y=![]() 得k=﹣1×1=﹣1;
得k=﹣1×1=﹣1;
②∵点A与点B关于原点中心对称,
∴B点坐标为(1,﹣1),
∴AB=2![]() ,
,
设P点坐标为(0,t),
当∠PAB=90°,则PA2+AB2=PB2,即12+(t﹣1)2+(2![]() )2=12+(t+1)2,解得t=2;
)2=12+(t+1)2,解得t=2;
当∠PBA=90°,则PB2+AB2=PA2,即12+(t+1)2+(2![]() )2=12+(t﹣1)2,解得t=﹣2;
)2=12+(t﹣1)2,解得t=﹣2;
当∠APB=90°,则PA2+PB2=AB2,即12+(t﹣1)2+12+(t+1)2=(2![]() )2,解得t=±
)2,解得t=±![]()
∴点P的所有可能的坐标是(0,![]() ),(0,﹣
),(0,﹣![]() ),(0,2),(0,﹣2).
),(0,2),(0,﹣2).

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目