题目内容
已知抛物线:y1=-| 1 | 2 |
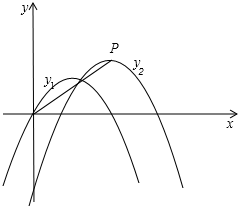 单位,得到抛物线y2,
单位,得到抛物线y2,(1)求抛物线y2的解析式.
(2)如图,抛物线y2的顶点为P,x轴上有一动点M,在y1、y2这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
分析:(1)直接利用二次函数平移的规律解答即可;
(2)假设符合条件的N点存在,利用平行四边形的性质和三角形全等,找出点N到x轴的距离,即抛物线的纵坐标,代入解析式,解方程解决问题.
(2)假设符合条件的N点存在,利用平行四边形的性质和三角形全等,找出点N到x轴的距离,即抛物线的纵坐标,代入解析式,解方程解决问题.
解答:解:(1)依题意把抛物线:y1=-
x2+2x=-
(x-2)2+2向右平移2个单位,再向上平移1个单位,得到y2=-
(x-4)2+3,
整理得y2=-
x2+4x-5;
(2)符合条件的N点存在.
如图:若四边形OPMN为符合条件的平行四边形,则OP∥MN,且OP=MN,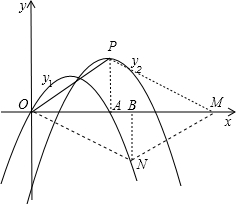
∴∠POA=∠BMN,作PA⊥x轴于点A,NB⊥x轴于点B
∴∠PAO=∠MBN=90°,
∴△POA≌△NMB(AAS),
∴PA=BN,
∵点P的坐标为(4,3),
∴NB=PA=3,
∵点N在抛物线y1、y2上,且P点为y1、y2的最高点
∴符合条件的N点只能在x轴下方,
①点N在抛物线y1上,则有:-
x2+2x=-3
解得:x=2-
x=2+
②点N在抛物线y2上,则有:-
(x-4)2+3=-3
解得:x=4-2
或x=4+2
∴符合条件的N点有四个:
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得y2=-
| 1 |
| 2 |
(2)符合条件的N点存在.
如图:若四边形OPMN为符合条件的平行四边形,则OP∥MN,且OP=MN,

∴∠POA=∠BMN,作PA⊥x轴于点A,NB⊥x轴于点B
∴∠PAO=∠MBN=90°,
∴△POA≌△NMB(AAS),
∴PA=BN,
∵点P的坐标为(4,3),
∴NB=PA=3,
∵点N在抛物线y1、y2上,且P点为y1、y2的最高点
∴符合条件的N点只能在x轴下方,
①点N在抛物线y1上,则有:-
| 1 |
| 2 |
解得:x=2-
| 10 |
| 10 |
②点N在抛物线y2上,则有:-
| 1 |
| 2 |
解得:x=4-2
| 3 |
| 3 |
∴符合条件的N点有四个:
|
点评:此题考查利用平移的规律求二次函数顶点式解析式,利用平行四边形的性质、三角形的全等与性质以及二次函数图象上点的坐标特征解决问题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 大小.
大小.