题目内容
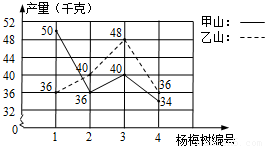
 为开发农业生态发展,王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
为开发农业生态发展,王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.(1)分别计算甲、乙两山样本的极差;
(2)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(3)试通过计算说明,哪个山上的杨梅产量较稳定?
分析:(1)利用极差的定义,从图中找到该组数据的最大值和最小值,相减即可;
(2)根据表中数据,利用平均数公式即可直接计算出甲、乙两山杨梅产量的样本平均数,利用样本平均数代替总体平均数即可估算出甲、乙两山杨梅的产量总和;
(3)计算出图中所示两组数据的方差,方差越小越稳定.
(2)根据表中数据,利用平均数公式即可直接计算出甲、乙两山杨梅产量的样本平均数,利用样本平均数代替总体平均数即可估算出甲、乙两山杨梅的产量总和;
(3)计算出图中所示两组数据的方差,方差越小越稳定.
解答:解:(1)甲山的样本的极差:50-34=16千克,
乙山的样本的极差:48-36=12千克.
(2)
=
(50+36+40+34)=40千克,
=
(36+40+48+36)=40千克;
甲、乙两山的产量总和为:100×98%×2×40=7840千克.
(3)S2甲=
[(50-40)2+(36-40)2+(40-40)2+(34-40)2]=38,
S2乙=
[(36-40)2+(40-40)2+(48-40)2+(36-40)2]=24,
∴S2甲>S2乙,
∴乙稳定.
乙山的样本的极差:48-36=12千克.
(2)
. |
| x甲 |
| 1 |
| 4 |
. |
| x乙 |
| 1 |
| 4 |
甲、乙两山的产量总和为:100×98%×2×40=7840千克.
(3)S2甲=
| 1 |
| 4 |
S2乙=
| 1 |
| 4 |
∴S2甲>S2乙,
∴乙稳定.
点评:本题考查了折线统计图、方差、平均数和极差,从图中找到所需的统计量是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目