题目内容
如图，AB∥CD，且∠1=115°，∠A=75°，则∠E的度数是
- A.30°
- B.50°
- C.40°
- D.60°
C
分析：由AB∥CD，∠A=75°可以得到∠ECD=∠A=75°，而∠1=115°，再利用三角形外角的性质即可求出∠E．
解答：∵AB∥CD，∠A=75°，∴∠ECD=∠A=75°，
∵∠1=115°，∴∠E=∠1-∠ECD=40°．
故选C．
点评：本题应用的知识点为：两直线平行，同位角相等；三角形的一个外角等于和它不相邻的两个内角的和．
分析：由AB∥CD，∠A=75°可以得到∠ECD=∠A=75°，而∠1=115°，再利用三角形外角的性质即可求出∠E．
解答：∵AB∥CD，∠A=75°，∴∠ECD=∠A=75°，
∵∠1=115°，∴∠E=∠1-∠ECD=40°．
故选C．
点评：本题应用的知识点为：两直线平行，同位角相等；三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
名校课堂系列答案
相关题目
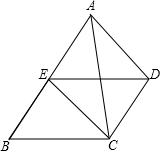如图，AB∥CD，且AB=2CD，E为AB的中点．
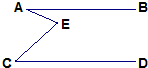18、如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是
11、如图，AB∥CD，且∠1=115°，∠A=75°，则∠E的度数是
13、如图，AB∥CD，且∠A=30°，∠C=25°，则∠E=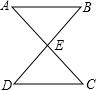
如图，AB∥CD，且AB=CD，则△ABE≌△CDE的根据是（ ）