题目内容
如图，AB是⊙O的直径，BC为⊙O的切线，∠ACB=40°，点P在边BC上，则∠PAB的度数可能为______（写出一个符合条件的度数即可）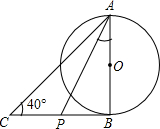
∵AB是⊙O的直径，BC为⊙O的切线，
∴AB⊥BC，
∴∠ABC=90°，
∴∠ACB=40°（已知），
∴∠CAB=50°（直角三角形的两个锐角互余）；
又∵点P在边BC上，
∴0＜∠PAB＜∠CAB，
∴∠PAB可以取49°，45°，40…
故答案可以是：45°
∴AB⊥BC，
∴∠ABC=90°，
∴∠ACB=40°（已知），
∴∠CAB=50°（直角三角形的两个锐角互余）；
又∵点P在边BC上，
∴0＜∠PAB＜∠CAB，
∴∠PAB可以取49°，45°，40…
故答案可以是：45°
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
8、如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为（ ）
0.1平方米）
如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为