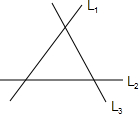题目内容
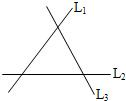
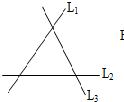 15、如图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选择的位置共有
15、如图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选择的位置共有4
个.分析:利用角平线性质知角平分线上的点到角两边距离相等,通过三角形内心为其内切圆的圆心来解得.
解答:解:根据三条路线构成的三角形知,三角形的内心为三角形内角角平分线的交点.
∵由三角形内心为该三角形内切圆的圆心,
∴所以符合货物中转站到各路的距离相等.
这样的点可找到一个.
外角平分线的交点,到三条公路的距离也相等,可找到三个.
故答案为:4.
∵由三角形内心为该三角形内切圆的圆心,
∴所以符合货物中转站到各路的距离相等.
这样的点可找到一个.
外角平分线的交点,到三条公路的距离也相等,可找到三个.
故答案为:4.
点评:本题考查角平分线性质,以及三角形内心为其内切圆的圆心解得.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
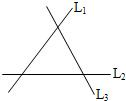 9、如图是三条两两相交的笔直公路,现要修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有( )个.
9、如图是三条两两相交的笔直公路,现要修建一个加油站,使它到三条公路的距离相等,这个加油站的位置共有( )个.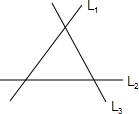 如图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选择的位置共有________个.
如图是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选择的位置共有________个.