题目内容
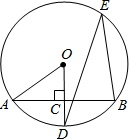 (2012•江津区模拟)如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(2012•江津区模拟)如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
分析:(1)根据垂径定理,得到
=
,再根据圆周角与圆心角的关系,得知∠E=
∠O,据此即可求出∠DEB的度数;
(2)由垂径定理可知,AB=2AC,在Rt△AOC中,OC=3,OA=5,由勾股定理求AC即可.
 |
| AD |
 |
| DB |
| 1 |
| 2 |
(2)由垂径定理可知,AB=2AC,在Rt△AOC中,OC=3,OA=5,由勾股定理求AC即可.
解答:解:(1)∵AB是⊙O的一条弦,OD⊥AB,
∴
=
,∴∠DEB=
∠AOD=
×52°=26°;
(2)∵AB是⊙O的一条弦,OD⊥AB,
∴AC=BC,即AB=2AC,
在Rt△AOC中,AC=
=
=4,
则AB=2AC=8.
∴
 |
| AD |
 |
| DB |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵AB是⊙O的一条弦,OD⊥AB,
∴AC=BC,即AB=2AC,
在Rt△AOC中,AC=
| OA2-OC2 |
| 52-32 |
则AB=2AC=8.
点评:本题考查了垂径定理,勾股定理及圆周角定理.关键是由垂径定理得出相等的弧,相等的线段,由垂直关系得出直角三角形,运用勾股定理.

练习册系列答案
相关题目
 B为一边作正方形ABCD.
B为一边作正方形ABCD.