题目内容
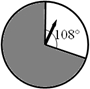如图，转动的转盘停止转动后，指针指向黑色区域的概率是分析：设圆的半径为R，根据圆的面积公式和扇形的面积公式得到圆的面积=πR2，黑色区域的面积=
=
πR2，然后用黑色区域的面积比圆的面积即可得到针指向黑色区域的概率．
| (360-108)•π•R2 |
| 360 |
| 7 |
| 10 |
解答：解：设圆的半径为R，
∴圆的面积=πR2，
黑色区域的面积=
=
πR2，
∴转动的转盘停止转动后，指针指向黑色区域的概率=
=
．
故答案为
．
∴圆的面积=πR2，
黑色区域的面积=
| (360-108)•π•R2 |
| 360 |
| 7 |
| 10 |
∴转动的转盘停止转动后，指针指向黑色区域的概率=
| ||
| πR2 |
| 7 |
| 10 |
故答案为
| 7 |
| 10 |
点评：本题考查了几何概率的求法：先求出整个图形的面积n，再计算某事件所占有的面积m，则这个事件的概率=
．也考查了扇形的面积公式．
| m |
| n |
练习册系列答案
相关题目
如图所示，转盘被等分成八个扇形，并在上面依次标有数字1，2，3，4，5，6，7，8．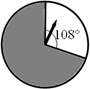
如图，转动的转盘停止转动后，指针指向黑色区域的概率是________．
