题目内容
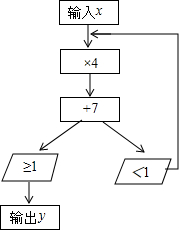 如图,是一个运算流程.
如图,是一个运算流程.
(1)分别计算x=2,-2时y的值.
(2)若需要经过一次运算,就能运算出y,求x的取值范围.
(3)若需要经过两次运算,也不能运算出y,求x的取值范围.
解:(1)由题意可知,当x=2时,y=4x+7=15;当x=-2时,y=4x+7=-1<1,
所以继续计算当把-1代入y=4x+7=3;
(2)若需要经过1次运算,才能运算出y,
则有不等式:4x+7≥1,
解得:x≥- ,
,
(3)由输入两次,也不能计算出y的值得:
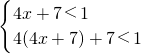 ,
,
解得:x<-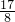 .
.
分析:根据所给的运算流程可知,若4x+7<1,则输出y=4(4x+7)+7,若4x+7≥1,则输出y=4x+7;若4(4x+7)+7<1,则继续进行上步的计算.
(1)x=2>1,则直接输出y=4x+7=15;x=-2<1,按照题中所给的算法运算即可;
(2)若需要经过1次运算,才能运算出y,则有不等式:4x+7≥1,即可解出x的取值范围;
(3)需要经过两次运算,都无法运算出y,即算出的y值小于1,列出x的不等式,求出不等式的解集即可得到x的范围.
点评:本题考查了不等式的应用,并考查了学生的阅读理解能力,解答本题的关键就是弄清楚题图给出的计算程序.
所以继续计算当把-1代入y=4x+7=3;
(2)若需要经过1次运算,才能运算出y,
则有不等式:4x+7≥1,
解得:x≥-
 ,
,(3)由输入两次,也不能计算出y的值得:
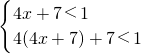 ,
,解得:x<-
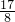 .
.分析:根据所给的运算流程可知,若4x+7<1,则输出y=4(4x+7)+7,若4x+7≥1,则输出y=4x+7;若4(4x+7)+7<1,则继续进行上步的计算.
(1)x=2>1,则直接输出y=4x+7=15;x=-2<1,按照题中所给的算法运算即可;
(2)若需要经过1次运算,才能运算出y,则有不等式:4x+7≥1,即可解出x的取值范围;
(3)需要经过两次运算,都无法运算出y,即算出的y值小于1,列出x的不等式,求出不等式的解集即可得到x的范围.
点评:本题考查了不等式的应用,并考查了学生的阅读理解能力,解答本题的关键就是弄清楚题图给出的计算程序.

练习册系列答案
相关题目
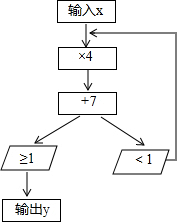 如图,是一个运算流程.
如图,是一个运算流程. 如图,是一个运算流程.
如图,是一个运算流程.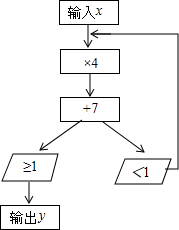 如图,是一个运算流程.
如图,是一个运算流程.
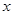 =2时,y= _____;当x=-2时,
=2时,y= _____;当x=-2时,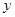 = ____.
= ____.
 =2时,y= _____;当x=-2时,
=2时,y= _____;当x=-2时,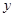 = ____.
= ____.