题目内容
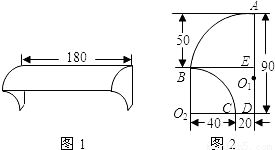
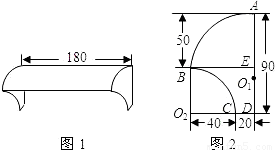
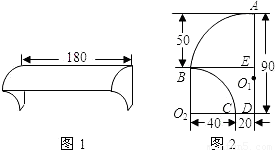
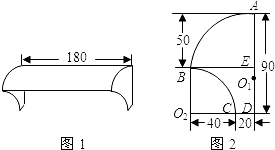
小亮家窗户上的遮雨罩是一种玻璃钢制品,它的顶部是圆柱侧面的一部分(如图1),它的侧面边缘上有两条圆弧(如图2),其中顶部圆弧AB的圆心O1在竖直边缘AD上,另一条圆弧BC的圆心O2在水平边缘DC的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题.(玻璃钢材料的厚度忽略不计,π取3.1416)(1)计算出弧AB所对的圆心角的度数(精确到0.01度)及弧AB的长度;(精确到0.1cm)
(2)计算出遮雨罩一个侧面的面积;(精确到1cm2)
(3)制做这个遮雨罩大约需要多少平方米的玻璃钢材料.(精确到0.1平方米)
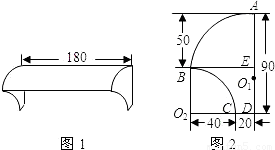
【答案】分析:(1)本题的关键是求出弧AB所在圆的半径.连接BO1,∠BO1E就是所求的弧AB所对的圆心角,在直角三角形BO1E中,已知了BE的长,我们可用直径表示出O1E和O1B,根据勾股定理求出半径的长,有了半径的长,就能用正弦函数求出∠BO1E的度数,也可根据弧长的公式求出弧AB的长;
(2)我们观察图可发现,遮雨罩的侧面的面积应该是扇形O1AB的面积+梯形O1BO2D的面积-扇形O2BC的面积,已知了弧AB,BC所对的圆心角,已知了弧AB,BC所在圆的半径,那么就能根据扇形的面积公式求出这两个扇形的面积,梯形O1BO2D中,(1)中已经得出O1A的值,那么就能求出O1D的长,它的另一个底边是半径O2B,高是O2D,所有的条件就都有了,那么就能求出侧面的面积了.
(3)遮雨罩的表面积=2个侧面的面积+顶部的面积,侧面的面积(2)中已经求出,顶部的面积实际是个矩形的面积,这个矩形的长是180m,宽是(1)中得出的弧AB的长,那么就能求出遮雨罩的表面积了,也就求出需要多少材料了.
解答:解:(1)易知BE=60,AE=50,连接O1B,设弧AB的半径为R.
在Rt△O1BE中,由勾股定理得:R2=602+(R-50)2.
解得:R=61.
∵sin∠BO1E=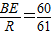 ,
,
∴∠BO1E≈79.61度.
∴弧AB的长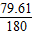 ×π×61≈84.8;
×π×61≈84.8;
(2)扇形O1AB的面积= ×84.8×61≈2586.4(cm2);
×84.8×61≈2586.4(cm2);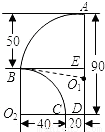
扇形O2BC的面积= ×π×402=400π≈1256.6(cm2);
×π×402=400π≈1256.6(cm2);
梯形O1BO2D的面积= ×(29+40)×60=2070(cm2);
×(29+40)×60=2070(cm2);
∴遮雨罩一个侧面的面积=扇形O1AB的面积+梯形O1BO2D的面积-扇形O2BC的面积
=2586.4+2070-1256.6≈3400(cm2);
(3)遮雨罩顶部的面积=84.8×180=15264(cm2).
∴遮雨罩的总面积=3400×2+15264=22064(cm2)≈2.2(m2).
制做这个遮雨罩大约需要2.2平方米玻璃钢材料.
点评:本题主要考查了扇形的面积公式,弧长的计算公式,以及解直角三角形等知识点的综合应用,求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.
(2)我们观察图可发现,遮雨罩的侧面的面积应该是扇形O1AB的面积+梯形O1BO2D的面积-扇形O2BC的面积,已知了弧AB,BC所对的圆心角,已知了弧AB,BC所在圆的半径,那么就能根据扇形的面积公式求出这两个扇形的面积,梯形O1BO2D中,(1)中已经得出O1A的值,那么就能求出O1D的长,它的另一个底边是半径O2B,高是O2D,所有的条件就都有了,那么就能求出侧面的面积了.
(3)遮雨罩的表面积=2个侧面的面积+顶部的面积,侧面的面积(2)中已经求出,顶部的面积实际是个矩形的面积,这个矩形的长是180m,宽是(1)中得出的弧AB的长,那么就能求出遮雨罩的表面积了,也就求出需要多少材料了.
解答:解:(1)易知BE=60,AE=50,连接O1B,设弧AB的半径为R.
在Rt△O1BE中,由勾股定理得:R2=602+(R-50)2.
解得:R=61.
∵sin∠BO1E=
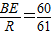 ,
,∴∠BO1E≈79.61度.
∴弧AB的长
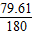 ×π×61≈84.8;
×π×61≈84.8;(2)扇形O1AB的面积=
 ×84.8×61≈2586.4(cm2);
×84.8×61≈2586.4(cm2);
扇形O2BC的面积=
 ×π×402=400π≈1256.6(cm2);
×π×402=400π≈1256.6(cm2);梯形O1BO2D的面积=
 ×(29+40)×60=2070(cm2);
×(29+40)×60=2070(cm2);∴遮雨罩一个侧面的面积=扇形O1AB的面积+梯形O1BO2D的面积-扇形O2BC的面积
=2586.4+2070-1256.6≈3400(cm2);
(3)遮雨罩顶部的面积=84.8×180=15264(cm2).
∴遮雨罩的总面积=3400×2+15264=22064(cm2)≈2.2(m2).
制做这个遮雨罩大约需要2.2平方米玻璃钢材料.
点评:本题主要考查了扇形的面积公式,弧长的计算公式,以及解直角三角形等知识点的综合应用,求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 0.1平方米)
0.1平方米)