Question

（2013•宝安区一模）已知矩形BEDG和矩形BNDQ中，BE=BN，DE=DN．
（1）将两个矩形叠合成如图10，求证：四边形ABCD是菱形；
（2）若菱形ABCD的周长为20，BE=3，求矩形BEDG的面积．

Answer 1

分析：（1）作AR⊥BC于R，AS⊥CD于S，根据题意先证出四边形ABCD是平行四边形，再由BC=CD得平行四边形ABCD是菱形；
（2）根据菱形的性质得出AD的长，进而得出AE的长，再利用矩形面积公式求出即可．

解答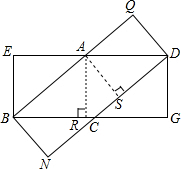：（1）答：四边形ABCD是菱形．
证明：作AR⊥BC于R，AS⊥CD于S，
由题意知：AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵矩形BEDG和矩形BNDQ中，BE=BN，DE=DN，
∴两个矩形全等，
∴AR=AS，
∵AR•BC=AS•CD，
∴BC=CD，
∴平行四边形ABCD是菱形；

（2）解：∵菱形ABCD的周长为20，
∴AD=AB=BC=CD=5，
∵BE=3，
∴AE=4，
∴DE=5+4=9，
∴矩形BEDG的面积为：3×9=27．

点评：此题主要考查了菱形的判定与性质以及勾股定理的应用，熟练掌握矩形的性质是解题关键．