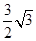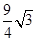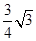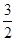题目内容
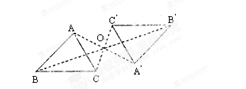
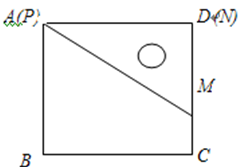
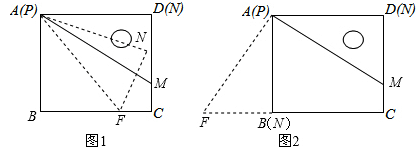
已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为______________.

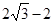 或
或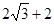 .
.试题分析:本题考查了旋转的性质、正方形的性质、以及解直角三角形.解答此题的关键也是难点在于区分△PMN的顶点不在直线BC上和在在直线BC上两种情况讨论求解.解直角三角形求出正方形的边长AD的长度,
由∠MPN=30°,MN=2,得AD=MN•cot∠MPN=2×cot30°=
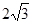 .然后分两种情况:①点F在BC上,点N不在BC上时,根据旋转的性质可得AF=AM,利用“HL”证明Rt△ABF和Rt△ADM全等,进而可得BF=DM,从而得到CF=CM=CD-DM=
.然后分两种情况:①点F在BC上,点N不在BC上时,根据旋转的性质可得AF=AM,利用“HL”证明Rt△ABF和Rt△ADM全等,进而可得BF=DM,从而得到CF=CM=CD-DM=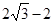 ;②点F、B都在直线BC上时,根据旋转的性质可得BF=MN=2,然后根据CF=BC+BF=
;②点F、B都在直线BC上时,根据旋转的性质可得BF=MN=2,然后根据CF=BC+BF=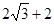 .所以CF的长为
.所以CF的长为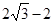 或
或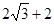 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目