题目内容
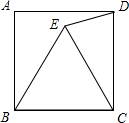 如图,等边三角形EBC在正方形ABCD内,连接DE,则∠CDE=________°.
如图,等边三角形EBC在正方形ABCD内,连接DE,则∠CDE=________°.
75
分析:正方形ABCD中,BC=CD,等边△BCE中,CE=BC,即可得CD=CE,∵∠DCE=90°-60°=30°,∴∠CDE=75°
解答:正方形ABCD中,BC=CD,
等边△BCE中,CE=BC,
∴CD=CE,
∵∠DCE=90°-60°=30°
,∴∠CDE= =75°
=75°
故答案为 75°.
点评:本题考查了正方形各边长相等、各内角为直角的性质,考查了等边三角形各内角为60°、各边长相等的性质,考查了三角形内角和为180°的性质,本题中求CD=CE是解题的关键.
分析:正方形ABCD中,BC=CD,等边△BCE中,CE=BC,即可得CD=CE,∵∠DCE=90°-60°=30°,∴∠CDE=75°
解答:正方形ABCD中,BC=CD,
等边△BCE中,CE=BC,
∴CD=CE,
∵∠DCE=90°-60°=30°
,∴∠CDE=
 =75°
=75°故答案为 75°.
点评:本题考查了正方形各边长相等、各内角为直角的性质,考查了等边三角形各内角为60°、各边长相等的性质,考查了三角形内角和为180°的性质,本题中求CD=CE是解题的关键.

练习册系列答案
相关题目
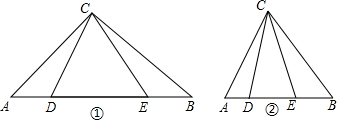
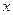 (0<
(0<
 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应 (0<
(0<
 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应 (0<
(0<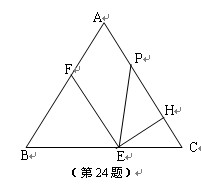
 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应