题目内容
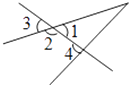
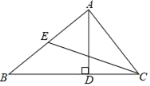
【题目】如图,在△ABC中,AD⊥BC,垂足为点D,CE是边AB上的中线,如果CD=BE,∠B=40°,那么∠BCE=_____度.
【答案】20.
【解析】
连接ED,再加上AD⊥BC,利用直角三角形斜边上的中线等于斜边的一半,很容易可以推出△ECD为等腰三角形,根据等腰三角形的性质:等边对等角,以及外角性质即可求出∠BCE的度数.
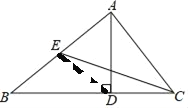
如图,连接ED,
∵AD⊥BC,
∴△ABD是直角三角形,
∵CE是边AB上的中线,
∴ED=![]() AB=BE,
AB=BE,
∴∠EDB=∠B=40°,
又∵CD=BE,
∴ED= CD,
∴∠DEC=∠DCE,
∵∠EDB是△DEC的外角,
∴∠EDB=∠DEC+∠DCE=2∠DCE=40°,
∴∠DCE=![]() ∠EDB=20°,
∠EDB=20°,
∵∠DCE即∠BCE,
∴∠BCE=20°.

练习册系列答案
相关题目