题目内容
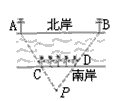
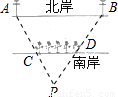
如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆．小丽站在离南岸边15米的点P处看北岸，发现北岸相邻的两根电线杆A、B，恰好被南岸的两棵树C、D遮住，并且在这两棵树之间还有三棵树，求河的宽度．
分析：根据题意画出图形，构造出△PCD∽△PAB，利用相似三角形的性质解题．
解答：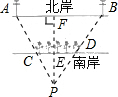
解：过P作PF⊥AB，交CD于E，交AB于F，如图所示：
设河宽为x米．
∵AB∥CD，
∴∠PDC=∠PBF，∠PCD=∠PAB，
∴△PDC∽△PBA，
∴
=
，
∴
=
，
依题意CD=20米，AB=50米，
∴
=
，
解得：x=22.5（米）．
答：河的宽度为22.5米．
解：过P作PF⊥AB，交CD于E，交AB于F，如图所示：设河宽为x米．
∵AB∥CD，
∴∠PDC=∠PBF，∠PCD=∠PAB，
∴△PDC∽△PBA，
∴
| AB |
| CD |
| PF |
| PE |
∴
| AB |
| CD |
| 15+x |
| 15 |
依题意CD=20米，AB=50米，
∴
| 20 |
| 50 |
| 15 |
| 15+x |
解得：x=22.5（米）．
答：河的宽度为22.5米．
点评：本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
练习册系列答案
阅读快车系列答案
相关题目
