题目内容
如图，直角梯形ABCD中，AB∥CD，∠DAB=90°，顶点A的坐标是（0，2），点B、C、D的坐标分别是（2，2）、（1，4）、（0，4），一次函数y=x+t的图象l随t的不同取值变化时，位于l的右下方由l和梯形的边围成的图形面积为S（阴影部分）．则能反映S与t（0≤t＜4）之间的函数图象是（ ）
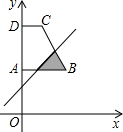
A． | B． | C． | D． |
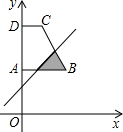
如图，设直线y=x+t与AB交于E，交BC于F，交OA于G，
∵B（2，2）、C（1，4）、
∴直线BC的解析式为y=-2x+6，
依题意得
，
∴
，
∴FH=
-2=
，
∵直线y=x+t，∴∠AGE=45°，
∴当y=0时，x=t，
∴OG=t，
∴AG=2-t，
∴AE=2-t，BE=t，
∴S△EFB=
×
×t=
t2，是关于t的二次函数，
图象应该是抛物线的一部分，
所给四个答案只有C正确．
故选C．
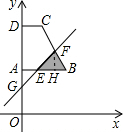
∵B（2，2）、C（1，4）、
∴直线BC的解析式为y=-2x+6，
依题意得
|
∴
|
∴FH=
| 6+2t |
| 3 |
| 2t |
| 3 |
∵直线y=x+t，∴∠AGE=45°，
∴当y=0时，x=t，
∴OG=t，
∴AG=2-t，
∴AE=2-t，BE=t，
∴S△EFB=
| 1 |
| 2 |
| 2t |
| 3 |
| 1 |
| 3 |
图象应该是抛物线的一部分，
所给四个答案只有C正确．
故选C．
练习册系列答案
优学名师名题系列答案
相关题目
的取值范围是 ，当
时，函数值y= .
