题目内容
 17、如图,在钝角△ABC中,点D,E分别是边AC,BC的中点,且DA=DE,那么下列结论错误的是( )
17、如图,在钝角△ABC中,点D,E分别是边AC,BC的中点,且DA=DE,那么下列结论错误的是( )分析:由DE是△ABC的中位线可以得出∠1=∠3,而AD=DE得出∠2=∠3,然后利用DA=DE=DC得出∠AEC是90°,从而得出△ABE≌△ACE,得出∠B=∠C,而不能得出∠3=∠B.
解答:解:∵点D,E分别是边AC,BC的中点,
∴DE是△ABC的中位线,则DE∥AB,
∴∠1=∠3
∵DA=DE
∴∠2=∠3,
∴∠1=∠2=∠3
又∵AD=DE=DC
∴∠2+∠C=∠3+∠DEC
∴∠AEC=90°
∴△ABE≌△ACE
∴∠B=∠C
∴结论错误的是∠3=∠B
故选D.
∴DE是△ABC的中位线,则DE∥AB,
∴∠1=∠3
∵DA=DE
∴∠2=∠3,
∴∠1=∠2=∠3
又∵AD=DE=DC
∴∠2+∠C=∠3+∠DEC
∴∠AEC=90°
∴△ABE≌△ACE
∴∠B=∠C
∴结论错误的是∠3=∠B
故选D.
点评:本题主要考查了三角形的中位线定理,等腰三角形的性质定理,等边对等角.由已知条件,联想到所学的定理,充分挖掘题目中的结论是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,在钝角△ABC中,∠A=30°,则tanA的值是( )
如图,在钝角△ABC中,∠A=30°,则tanA的值是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、无法确定 |
 26、如图,在钝角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE.有下列结论:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正确的结论有( )个.
26、如图,在钝角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE.有下列结论:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正确的结论有( )个.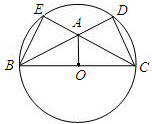 ,连接AO、BE、DC.
,连接AO、BE、DC. 23、如图,在钝角△ABC中,AB=AC,以BC为直径作⊙O,⊙O与BA、CA的延长线分别交于E、D两点,连接AO、DB、EC,试写出图中三对全等三角形,并对其中一对全等三角形进行证明.
23、如图,在钝角△ABC中,AB=AC,以BC为直径作⊙O,⊙O与BA、CA的延长线分别交于E、D两点,连接AO、DB、EC,试写出图中三对全等三角形,并对其中一对全等三角形进行证明.