题目内容
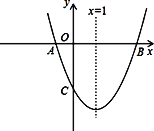
【题目】在直角△ABC中，∠ACB=90°，点E在AC边上，连结BE，作∠ACF=∠CBE交AB于点F，同时点D在BE上，且CD⊥AB．
（1）已知：如图，
=1，
．
①求证：△ACF≌△BCD．
②求
的值．
（2）若=2，
，则的值是多少（直接写出结果）
【答案】
（1）2，
（2）
【解析】
试题分析：（1）①根据等腰三角形的性质和全等三角形的判定证明即可；
②根据相似三角形的性质解答即可；
（2）根据②结论和图中条件解答即可．
试题解析：
证明：（1）①∵∠ACB=90°，
，CG⊥AB，
由等腰三角形的三线合一的性质可得：CD是∠ACB的角平分线，∠BCD=45°，
在△CAF与△BCD中，
，
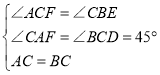∴△ACF≌△BCD；
②由①可知：∠AFC=∠CDB，
∴∠CFB=∠CDE，
∵∠CBF=∠ECD=45°，
∴△CDE∽△BFC，
∴
=2；
（2）∵，
∵
，
，
∴．
练习册系列答案
相关题目
