题目内容
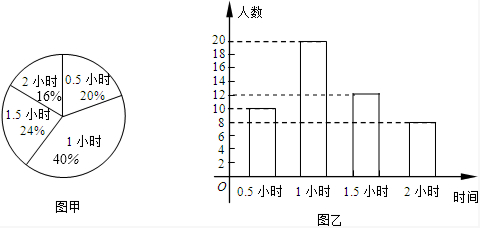
(2013•峨眉山市二模)为增强学生的身体素质,教育行政部门规定每个学生每天体育锻炼时间不少于1小时.某校为了解学生参加体育锻炼的情况,对初三(5)班学生参加体育锻炼的时间进行调查,并将调查结果绘制成如两幅不完整的统计图,如图甲和图乙

(1)请将条形统计图补充完整;
(2)根据图中的信息填空:初三(5)班共有
(3)从初三(5)班的学生中随机抽出一个学生进行调查,抽到学生参加体育锻炼时间不少于1小时的概率是多少?

(1)请将条形统计图补充完整;
(2)根据图中的信息填空:初三(5)班共有
50
50
人;体育锻炼时间的众数是1
1
小时;本次调查的学生参加体育锻炼的平均活动时间是1.18
1.18
;(3)从初三(5)班的学生中随机抽出一个学生进行调查,抽到学生参加体育锻炼时间不少于1小时的概率是多少?
分析:(1)根据0.5小时的人数是10,占20%,得出总人数,再用总人数、频率、频数、所占的百分比之间的关系,即可求出答案,从而补全统计图;
(2)根据众数的定义和平均数的计算公式分别进行计算,即可求出答案;
(3)把参加体育锻炼时间不少于1小时的人数加起来,再除以总人数,即可得出参加体育锻炼时间不少于1小时的概率.
(2)根据众数的定义和平均数的计算公式分别进行计算,即可求出答案;
(3)把参加体育锻炼时间不少于1小时的人数加起来,再除以总人数,即可得出参加体育锻炼时间不少于1小时的概率.
解答:解:(1)∵0.5小时的人数是10,占20%,
∴总人数是
=50(人),
∴1.5小时的人数是50×24%=12(人),
2小时的人数所占的百分比是
×100%=16%,
1小时的人数所占的百分比是
×100%=40%,
补图如下:
(2)根据题意得:
总人数是
=50(人),
1小时出现的人数最多,出现了20次,
则体育锻炼时间的众数是1小时,
本次调查的学生参加体育锻炼的平均活动时间是(0.5×10+1×20+1.5×12+2×8)÷50=1.18(小时);
(3)根据题意得:
抽到学生参加体育锻炼时间不少于1小时的概率是:
×100%=80%.
故答案为:50,1,1.18.
∴总人数是
| 10 |
| 20% |
∴1.5小时的人数是50×24%=12(人),
2小时的人数所占的百分比是
| 8 |
| 50 |
1小时的人数所占的百分比是
| 20 |
| 50 |
补图如下:

(2)根据题意得:
总人数是
| 10 |
| 20% |
1小时出现的人数最多,出现了20次,
则体育锻炼时间的众数是1小时,
本次调查的学生参加体育锻炼的平均活动时间是(0.5×10+1×20+1.5×12+2×8)÷50=1.18(小时);
(3)根据题意得:
抽到学生参加体育锻炼时间不少于1小时的概率是:
| 20+12+8 |
| 50 |
故答案为:50,1,1.18.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
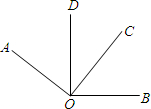 (2013•峨眉山市二模)如图所示,已知∠BOC=55°,∠AOC=∠BOD=90°,则∠AOD为( )
(2013•峨眉山市二模)如图所示,已知∠BOC=55°,∠AOC=∠BOD=90°,则∠AOD为( )