题目内容
 某学校锅炉房建有一个储煤库,开学初购进一批煤,按每天用煤0.6吨计算,一学期(按150天计)刚好用完,若每天的耗煤量为x(吨),那么这批煤能维持y(天).
某学校锅炉房建有一个储煤库,开学初购进一批煤,按每天用煤0.6吨计算,一学期(按150天计)刚好用完,若每天的耗煤量为x(吨),那么这批煤能维持y(天).(1)求y与x之间的函数关系式;
(2)在给定的坐标系中,作出(1)中求出的函数图象;
(3)若每天节约0.1吨煤,这批煤能维持多少天?
分析:(1)首先求得煤的总量,然后利用耗煤量乘以天数等于煤总量可得函数关系式即可;
(2)确定函数关系式后在坐标系中作出图象即可;
(3)将每天的用煤量代入求得的函数解析式即可求解.
(2)确定函数关系式后在坐标系中作出图象即可;
(3)将每天的用煤量代入求得的函数解析式即可求解.
解答:解:(1)煤的总量为:0.6×150=90吨,
∵x•y=90
∴y=
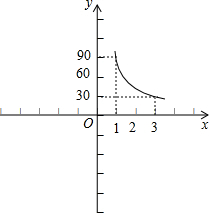
(2)函数的图象为:
(3)∵每天节约0.1吨煤,
∴每天的用煤量为0.6-0.1=0.5吨,
∴y=
=
=180天,
∴这批煤能维持180天.
∵x•y=90
∴y=
| 90 |
| x |
(2)函数的图象为:

(3)∵每天节约0.1吨煤,
∴每天的用煤量为0.6-0.1=0.5吨,
∴y=
| 90 |
| x |
| 90 |
| 0.5 |
∴这批煤能维持180天.
点评:本题考查了反比例函数的应用,熟悉两个变量之间的关系是解决本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 某学校锅炉房建有一个储煤库,开学初购进一批煤,按每天用煤0.6吨计算,一学期(按150天计)刚好用完,若每天的耗煤量为x(吨),那么这批煤能维持y(天).
某学校锅炉房建有一个储煤库,开学初购进一批煤,按每天用煤0.6吨计算,一学期(按150天计)刚好用完,若每天的耗煤量为x(吨),那么这批煤能维持y(天).