题目内容
(2001•昆明)平面上A、B两点到直线l的距离分别是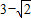 和
和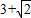 ,则线段AB的中点C到直线l的距离是( )
,则线段AB的中点C到直线l的距离是( )A.3
B.
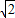
C.3或
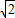
D.以上答案都不对
【答案】分析:此题应该分A,B在直线l的同侧和异侧两种情况进行分析.
解答: 解:本题要分两种情况讨论
解:本题要分两种情况讨论
(1)如图(一)A,B在直线l的同侧时
∵C是AB的中点
∴CD是梯形AEFB的中位线
∴CD= (AE+BF)=
(AE+BF)= (3-
(3-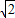 +3+
+3+ )=3.
)=3.
(2)如图(二)A,B在直线l的两侧时
连接AF,EB,延长CD交AF与G,反向延长CD交BE于H
∵AE⊥EF,BF⊥EF,CD⊥EF,C为AB的中点
∴AE∥CD∥BF,AC=BC,ED=DF
∴GH是梯形AEBF的中位线
∴GH= (AE+BF)=
(AE+BF)= (3-
(3- +3+
+3+ )=3
)=3
在△ABF中,
∵AC=BC,HG∥BF
∴CG是△ABF的中位线
∴CG= BF=
BF= (3-
(3- )
)
同理,DH= BF=
BF= (3+
(3+ )
)
CD=GH-CG-DH=3- (3-
(3- )-
)- (3+
(3+ )=
)=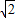
∴线段AB的中点C到直线l的距离是3或 .
.
故选C.
点评:本题考查了三角形及梯形中位线的性质,在解答时一定要分两种情况讨论,不要漏解.
解答:
 解:本题要分两种情况讨论
解:本题要分两种情况讨论(1)如图(一)A,B在直线l的同侧时
∵C是AB的中点
∴CD是梯形AEFB的中位线
∴CD=
 (AE+BF)=
(AE+BF)= (3-
(3-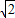 +3+
+3+ )=3.
)=3.(2)如图(二)A,B在直线l的两侧时
连接AF,EB,延长CD交AF与G,反向延长CD交BE于H
∵AE⊥EF,BF⊥EF,CD⊥EF,C为AB的中点
∴AE∥CD∥BF,AC=BC,ED=DF
∴GH是梯形AEBF的中位线
∴GH=
 (AE+BF)=
(AE+BF)= (3-
(3- +3+
+3+ )=3
)=3在△ABF中,
∵AC=BC,HG∥BF
∴CG是△ABF的中位线
∴CG=
 BF=
BF= (3-
(3- )
)同理,DH=
 BF=
BF= (3+
(3+ )
)CD=GH-CG-DH=3-
 (3-
(3- )-
)- (3+
(3+ )=
)=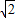
∴线段AB的中点C到直线l的距离是3或
 .
.故选C.
点评:本题考查了三角形及梯形中位线的性质,在解答时一定要分两种情况讨论,不要漏解.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 和
和 ,则线段AB的中点C到直线l的距离是( )
,则线段AB的中点C到直线l的距离是( )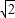
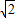
 和
和 ,则线段AB的中点C到直线l的距离是( )
,则线段AB的中点C到直线l的距离是( )