题目内容
【题目】(1)甲地的海拔高度是![]() ,乙地的海拔高度是甲地海拔高度的3倍多
,乙地的海拔高度是甲地海拔高度的3倍多![]() ,丙地的海拔高度比甲地的海拔高度低
,丙地的海拔高度比甲地的海拔高度低![]() ,列式计算乙、丙两地的高度差.
,列式计算乙、丙两地的高度差.
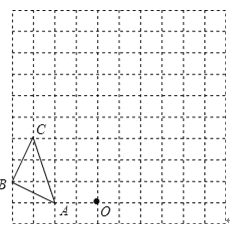
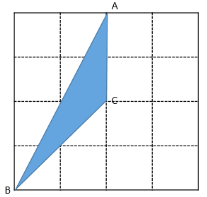
(2)在4×4的方格纸中,三角形![]() 的三个顶点都在格点上,将图中的三角形
的三个顶点都在格点上,将图中的三角形![]() 绕着点
绕着点![]() 按顺时针方向旋转90°,画出旋转后的三角形.
按顺时针方向旋转90°,画出旋转后的三角形.
【答案】(1)(2h+50)m;(2)答案见解析
【解析】
(1)根据乙地的海拔高度是甲地海拔高度的3倍多![]() ,列出乙地海拔为(3h+20)m;根据,丙地的海拔高度比甲地的海拔高度低
,列出乙地海拔为(3h+20)m;根据,丙地的海拔高度比甲地的海拔高度低![]() 。列出丙地海拔为(h-30)m,然后用乙地海拔减去丙地海拔,求解;(2)根据网格结构找出点A、B绕着点C按顺时针方向旋转90°后的对应点的位置,再与点C顺次连接即可.
。列出丙地海拔为(h-30)m,然后用乙地海拔减去丙地海拔,求解;(2)根据网格结构找出点A、B绕着点C按顺时针方向旋转90°后的对应点的位置,再与点C顺次连接即可.
解:(1)由题意可得:乙地海拔为(3h+20)m,丙地海拔为(h﹣30)m,
∴(3h+20)﹣(h﹣30)
=3h+20﹣h+30
=2h+50,
答:乙、丙两地的高度差为(2h+50)m
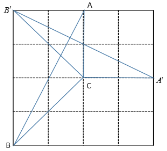
(2)如图:

【题目】大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?