题目内容
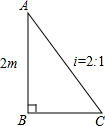高速公路旁有一矩形坡面，其横截面如下图所示，公路局为了美化公路沿线环境，决定把该矩形坡面平均分成11段，相间的种草与栽花．已知该矩形坡面的长为550米，铅直高度AB为2米，坡度为2：1，若种草每平方米需投20元，栽花每平方米需投资15元，求公路局将这一坡面美化最少需投资多少元？（结果保留三个有效数字）
解：Rt△ABC中，AC坡度比为2：1，AB：BC=2：1．
∴AB：AC=2：
．
∴AC=米．
∴矩形坡面的面积=×550≈1229.8平方米．
每段的坡面的面积就是1229.8÷11≈111.8平方米．
由于是相间种草和栽花，因此美化的方案可分为两种：
1：种5行花，种6行草
2：种6行花，种5行草．
因为草的每平米投资比花多．
∴2方案投资较少．
为：6×15×111.8+5×20×111.8≈21242元．
答：最少要投资21242元．
分析：本题先要求出坡AC的长，然后可根据栽种的不同方案来确定最少的投资方案．
点评：本题是将实际问题转化为直角三角形中的数学问题，可把条件和问题放到直角三角形中，进行解决．
∴AB：AC=2：
．∴AC=
米．∴矩形坡面的面积=
×550≈1229.8平方米．每段的坡面的面积就是1229.8÷11≈111.8平方米．
由于是相间种草和栽花，因此美化的方案可分为两种：
1：种5行花，种6行草
2：种6行花，种5行草．
因为草的每平米投资比花多．
∴2方案投资较少．
为：6×15×111.8+5×20×111.8≈21242元．
答：最少要投资21242元．
分析：本题先要求出坡AC的长，然后可根据栽种的不同方案来确定最少的投资方案．
点评：本题是将实际问题转化为直角三角形中的数学问题，可把条件和问题放到直角三角形中，进行解决．
练习册系列答案
相关题目
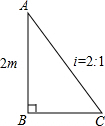高速公路旁有一矩形坡面，其横截面如下图所示，公路局为了美化公路沿线环境，决定把该矩形坡面平均分成11段，相间的种草与栽花．已知该矩形坡面的长为550米，铅直高度AB为2米，坡度为2：1，若种草每平方米需投20元，栽花每平方米需投资15元，求公路局将这一坡面美化最少需投资多少元？（结果保留三个有效数字）
