题目内容
阅读下面材料：解答问题
为解方程 (x2－1)2－5 (x2－1)＋4＝0，我们可以将（x2－1）看作一个整体，然后设 x2－1＝y，那么原方程可化为 y2－5y＋4＝0，解得y1＝1，y2＝4．
当y＝1时，x2－1＝1，∴x2＝2，∴x＝±；当y＝4时，x2－1＝4，∴x2＝5，∴x＝±，
故原方程的解为 x1＝，x2＝－，x3＝，x4＝－．
上述解题方法叫做换元法；
请利用换元法解方程．(x 2－x)2 － 4 (x 2－x)－12＝0
【答案】
设 x2－x＝y，则原方程可化为 y2－4y-12＝0，解得y1＝6，y2＝-2．
当y＝6时，x2－x＝6，∴x2-x-6＝0，∴x1＝3，x2=-2；[来源:]
当y＝-2时，x2－x＝-2，∴x2-x+2＝0，∵△＝(-1)2-4×1×2=-7＜0，∴原方程无实数根.
∴原方程的解为 x1＝3，x2＝－2．
【解析】略
练习册系列答案
相关题目
；当y＝4时，x2－1＝4，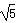
，