题目内容
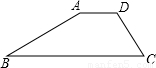
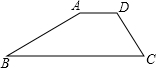
如图,某海埂的横断面是梯形,坎上底AD为4米,近水面(斜坡AB)的坡度i=1:| 3 |
 (斜坡CD)的坡度为i=1:1,
(斜坡CD)的坡度为i=1:1,求(1)斜坡AB的坡角(2)坎底宽BC和斜坡CD的长.
分析:(1)根据斜坡AB的坡度可以求得斜边AB的坡角的正切值,即可解题;
(2)根据AB和坡角即可求得AE、BE的长,进而根据CD的坡度求得FC的长度,即可求得BC的值,根据DF、FC即可求得CD的值.
(2)根据AB和坡角即可求得AE、BE的长,进而根据CD的坡度求得FC的长度,即可求得BC的值,根据DF、FC即可求得CD的值.
解答: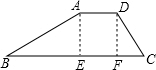 解:作AE⊥BC、DF⊥BC,
解:作AE⊥BC、DF⊥BC,
(1)则AE:BE=1:
,
∴tan∠ABE=
,
∠ABE=30°;
(2)∵AB=12米,
∴AE的长为6米,BE的长为6
米,
AE=DF=6,CD的坡度为1:1,
∴DF=FC=6,
∴BC=6
+4+6=(6
+10)米,
CD=
=6
米.
 解:作AE⊥BC、DF⊥BC,
解:作AE⊥BC、DF⊥BC,(1)则AE:BE=1:
| 3 |
∴tan∠ABE=
| ||
| 3 |
∠ABE=30°;
(2)∵AB=12米,
∴AE的长为6米,BE的长为6
| 3 |
AE=DF=6,CD的坡度为1:1,
∴DF=FC=6,
∴BC=6
| 3 |
| 3 |
CD=
| DF2+FC2 |
| 2 |
点评:本题考查了勾股定理在直角三角形中的运用,直角三角形中三角函数值的运用,考查了坡度的求值.

练习册系列答案
相关题目
 ,斜坡AB的长度为12米,背水面
,斜坡AB的长度为12米,背水面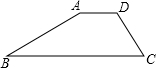 (斜坡CD)的坡度为i=1:1,
(斜坡CD)的坡度为i=1:1,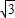 ,斜坡AB的长度为12米,背水面(斜坡CD)的坡度为i=1:1,
,斜坡AB的长度为12米,背水面(斜坡CD)的坡度为i=1:1,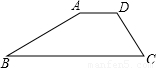
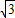 ,斜坡AB的长度为12米,背水面(斜坡CD)的坡度为i=1:1,
,斜坡AB的长度为12米,背水面(斜坡CD)的坡度为i=1:1,