题目内容
张老师为了从平时在班级里数学成绩比较优秀的王军、张成两位同学中选拔一个参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:
| 次数成绩姓名 | 第1 次 | 第2 次 | 第3 次 | 第4 次 | 第5 次 | 第6 次 | 第7 次 | 第8 次 | 第9 次 | 第10 次 |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
(1)填写完成下表
| 平均成绩 | 中位数 | 众数 | |
| 王 军 | 80 | 79.5 | |
| 张 成 | 80 | 80 |
S2张;
(3)平均差是总体所有单位的平均值与其算术平均数的离差绝对值的算术平均数.平均差是反映各标志值与算术平均数之间的平均差异.平均差异大,表明各标志值与算术平均数的差异程度越大,该算术平均数的代表性就越小;
试求王军与张成的平均差,哪个的算术平均数更具有代表性.
(4)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
解:(1)王军的众数为78 张成的中位数为80;
(2)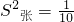 [(86-80)2+(80-80)2+L+(75-80)2],
[(86-80)2+(80-80)2+L+(75-80)2],
=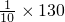 ,
,
=13;
(3)王军的平均差=110(|68-80|+|80-80|+|75-80|)=4,
张成的平均差=110(|86-80|+|80-80|+|75-80|)=3.6,
张成的平均差<王军的平均差,
所以张成的算术平均数更具有代表性;
(4)①王军、张成两位同学平均成绩相同,但S2张<S2王,说明张成的成绩较稳定,所以选择张成.
或:②王军、张成两位同学的平均成绩相同,但在后三次测验中王军的成绩有较大的提高,所以选择王军.
分析:(1)本题根据众数、中位数的定义即可求出结果.
(2)本题需根据方差的计算结果求出答案.
(3)本题须先求出王军和张成的平均差即可得出谁的算术平均数更具有代表性.
(4)本题须比较出王军与张成的方差,然后根据两人的后三次测验的成绩即可得出结果.
点评:本题主要考查了方差的有关概念,在解题时要能根据方差的计算公式求出一组数据的方差是本题的关键.
(2)
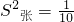 [(86-80)2+(80-80)2+L+(75-80)2],
[(86-80)2+(80-80)2+L+(75-80)2],=
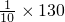 ,
,=13;
(3)王军的平均差=110(|68-80|+|80-80|+|75-80|)=4,
张成的平均差=110(|86-80|+|80-80|+|75-80|)=3.6,
张成的平均差<王军的平均差,
所以张成的算术平均数更具有代表性;
(4)①王军、张成两位同学平均成绩相同,但S2张<S2王,说明张成的成绩较稳定,所以选择张成.
或:②王军、张成两位同学的平均成绩相同,但在后三次测验中王军的成绩有较大的提高,所以选择王军.
分析:(1)本题根据众数、中位数的定义即可求出结果.
(2)本题需根据方差的计算结果求出答案.
(3)本题须先求出王军和张成的平均差即可得出谁的算术平均数更具有代表性.
(4)本题须比较出王军与张成的方差,然后根据两人的后三次测验的成绩即可得出结果.
点评:本题主要考查了方差的有关概念,在解题时要能根据方差的计算公式求出一组数据的方差是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:
利用表中提供的数据,解答下列问题:
(1)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S王2=33.2,请你帮助张老师计算张成10次测验成绩的方差S张2;
(2)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 | |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
(1)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S王2=33.2,请你帮助张老师计算张成10次测验成绩的方差S张2;
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | 80 |
张老师为了从平时在班级里数学成绩比较优秀的王军、张成两位同学中选拔一个参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:
利用上表中提供的数据,解答下列问题:
(1)填写完成下表
(2)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S2王=33.2,请你帮助张老师计算张成10次测验成绩的方差
S2张;
(3)平均差是总体所有单位的平均值与其算术平均数的离差绝对值的算术平均数.平均差是反映各标志值与算术平均数之间的平均差异.平均差异大,表明各标志值与算术平均数的差异程度越大,该算术平均数的代表性就越小;
试求王军与张成的平均差,哪个的算术平均数更具有代表性.
(4)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
| 次数成绩姓名 | 第1 次 |
第2 次 |
第3 次 |
第4 次 |
第5 次 |
第6 次 |
第7 次 |
第8 次 |
第9 次 |
第10 次 |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
(1)填写完成下表
| 平均成绩 | 中位数 | 众数 | |
| 王 军 | 80 | 79.5 | |
| 张 成 | 80 | 80 |
S2张;
(3)平均差是总体所有单位的平均值与其算术平均数的离差绝对值的算术平均数.平均差是反映各标志值与算术平均数之间的平均差异.平均差异大,表明各标志值与算术平均数的差异程度越大,该算术平均数的代表性就越小;
试求王军与张成的平均差,哪个的算术平均数更具有代表性.
(4)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:
利用表中提供的数据,解答下列问题:
(1)填写完成下表:
(2)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S王2=33.2,请你帮助张老师计算张成10次测验成绩的方差S张2;
(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 | |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | 80 |
(1)填写完成下表:
(2)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S王2=33.2,请你帮助张老师计算张成10次测验成绩的方差S张2;
(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下:
| | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
(1)填写完成下表:
| | 平均成绩 | 中位数 | 众数 |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | | 80 |
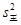 =33.2请你帮助张老师计算张成10次测验成绩的方差
=33.2请你帮助张老师计算张成10次测验成绩的方差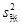 。
。(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由。