题目内容
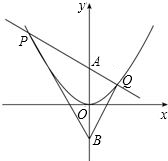
 如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数y=
如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数y=| 1 |
| x |
| 4 |
| x |
| 1 |
| x |
(1)当点P的坐标为(1,0)时,求△ABC的面积;
(2)当点P的坐标为(1,0)时,在y轴上是否存在一点Q,使A、C、Q三点为顶点的三角形△QAC为等腰三角形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
(3)请你连接QA和OC,当点P的坐标为(t,O)时,△ABC的面积是否随t的值的变化而变化?请说明理由.
分析:(1)根据点P的坐标和函数的解析式可以分别求得点A、B、C的坐标,进一步求得三角形的面积;
(2)分类讨论:①以AC为底的等腰△AOQ;②以AQ为底的等腰△AOQ;③以QC为底的等腰△AOQ;
(3)根据(1)中的方法进行求解,看最后的结果是否为一个定值即可.
(2)分类讨论:①以AC为底的等腰△AOQ;②以AQ为底的等腰△AOQ;③以QC为底的等腰△AOQ;
(3)根据(1)中的方法进行求解,看最后的结果是否为一个定值即可.
解答:解:(1)根据题意,得点A、B的横坐标和点P的横坐标相等,即为1.
∵点A在函数y=
(x>0)的双曲线上,
∴A点纵坐标是:yA=
=1,
∵点B在函数
(x>0)的图象上,
∴B点的纵坐标是:yB=
=4.
∵BC∥x轴,
∴点C、B的纵坐标相等,即yB=yC=4.
∵点C在函数y=
(x>0)的双曲线上,
∴C点横坐标是:xC=
=
,
∴AB=3,BC=
,
∴S△ABC=
AB•BC=
×3×
=
,即△ABC的面积是
;
(2)设Q(0,y).由(1)知,A(1,1),C(
,4).
①当以AC为底时,QA=QC,则
=
,解得,y=
,即Q1(0,
);
②当以AQ为底时,QC=AC,即
=
,解得,y=4+
或y=4-
,即Q2(0,4+
),Q3(0,4-
);
③当以CQ为底时,QA=AC,即
=
,解得,y=
,或y=
,即Q4(0,
),Q5(0,
);
综上所述,符合条件的点Q的坐标分别是:Q1(0,
),Q2(0,4+
),Q3(0,4-
),Q4(0,
),Q5(0,
);
(3)△ABC的面积不随t的值的变化而变化.理由如下:
∵根据(1)中的思路,可以分别求得点A(t,
),B(t,
),C(
,
).
∴AB=
,BC=
t,
∴△ABC的面积是
.
∴△ABC的面积不会随着t的变化而变化.
∵点A在函数y=
| 1 |
| x |
∴A点纵坐标是:yA=
| 1 |
| 1 |
∵点B在函数
| 4 |
| x |
∴B点的纵坐标是:yB=
| 4 |
| 1 |
∵BC∥x轴,
∴点C、B的纵坐标相等,即yB=yC=4.
∵点C在函数y=
| 1 |
| x |
∴C点横坐标是:xC=
| 1 |
| yC |
| 1 |
| 4 |
∴AB=3,BC=
| 3 |
| 4 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 8 |
| 9 |
| 8 |
(2)设Q(0,y).由(1)知,A(1,1),C(
| 1 |
| 4 |
①当以AC为底时,QA=QC,则
| 12+(y-1)2 |
(
|
| 75 |
| 32 |
| 75 |
| 32 |
②当以AQ为底时,QC=AC,即
(
|
(1-
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
③当以CQ为底时,QA=AC,即
| 12+(y-1)2 |
(1-
|
4+
| ||
| 4 |
4-
| ||
| 4 |
4+
| ||
| 4 |
4-
| ||
| 4 |
综上所述,符合条件的点Q的坐标分别是:Q1(0,
| 75 |
| 32 |
| ||
| 2 |
| ||
| 2 |
4+
| ||
| 4 |
4-
| ||
| 4 |
(3)△ABC的面积不随t的值的变化而变化.理由如下:
∵根据(1)中的思路,可以分别求得点A(t,
| 1 |
| t |
| 4 |
| t |
| t |
| 4 |
| 4 |
| t |
∴AB=
| 3 |
| t |
| 3 |
| 4 |
∴△ABC的面积是
| 9 |
| 8 |
∴△ABC的面积不会随着t的变化而变化.
点评:本题考查了反比例函数综合题.解答此题时要能够根据解析式熟练地求得各个点的坐标,根据坐标计算相关线段的长度.

练习册系列答案
相关题目
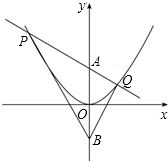 于P,Q两点.
于P,Q两点.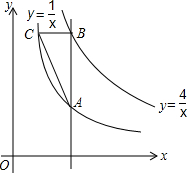 如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数
如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数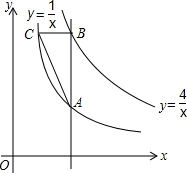 如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数
如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数 的图象于点A,交函数
的图象于点A,交函数 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交
 于P,Q两点.
于P,Q两点.