题目内容
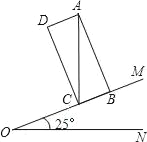
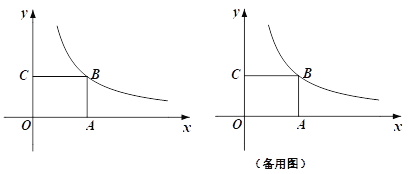
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,
,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 的最小值
的最小值![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 、
、![]()
【解析】
(1)根据已知得出点![]() 的坐标为
的坐标为![]() ,从而得出
,从而得出![]() .设点
.设点![]() 的纵坐标为
的纵坐标为![]() ,
,
由![]() ,得出m的值,即可得出P的坐标.
,得出m的值,即可得出P的坐标.
(2)过点![]() 作直线
作直线![]() 轴.由(1)知,点
轴.由(1)知,点![]() 的纵坐标为
的纵坐标为![]() ,从而得出点
,从而得出点![]() 在直线
在直线![]() 上.作点
上.作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则![]() .连接
.连接![]() 交直线
交直线![]() 于点
于点![]() ,此时
,此时![]() 的值最小,根据勾股定理即可得出结论.
的值最小,根据勾股定理即可得出结论.
(3)画出图形,根据图形直接写出结论即可.
(1)∵四边形![]() 是矩形,
是矩形,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,
∴![]() ,
,
∴![]() .
.

∴![]() ,
,
设点![]() 的纵坐标为
的纵坐标为![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
当点![]() 在这个反比例函数图像上时,则
在这个反比例函数图像上时,则![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(2)过点![]() 作直线
作直线![]() 轴.
轴.
由(1)知,点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则![]() .
.
连接![]() 交直线
交直线![]() 于点
于点![]() ,此时
,此时![]() 的值最小,
的值最小,
则![]() 的最小值
的最小值![]() .
.
(3)点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 、
、![]() .
.



【题目】暑假期间,小李同学勤工俭学购进一批矿泉水和运动饮料在运动场进行销售,其进价与售价如下表:
进价(元/瓶) | 售价(元/瓶) | |
矿泉水 | 0.75 | 2 |
运动饮料 | 3 | 4 |
(1)若小李同学购进矿泉水和运动饮料共 30 瓶,用去了 67.5 元,并且全部售完,问小李同学在该买卖中赚了多少钱?
(2)为了进一步满足同学们的需求,小李同学决定用不超过 400 元的资金购进矿泉水和运动饮料共200 瓶,问最多购进多少瓶运动饮料?
(3)小李同学赚钱后,为了回报社会,买了一批书籍送给贫困山区的孩子,如果分给每位孩子 4 本书,那么剩下 10 本书;如果分给每位孩子 5 本书,那么最后一位孩子分得的书不足 4 本,但至少1本,则小李同学买了多少本书?
【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?