题目内容
【题目】如图,在平面直角坐标系中,已知抛物线![]() 过
过![]() 三点,点A的坐标是
三点,点A的坐标是![]() ,点C的坐标是
,点C的坐标是![]() ,动点P在抛物线上.
,动点P在抛物线上.
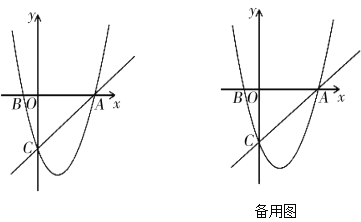
(1)b=___,c=____,点B的坐标为______;
(2)是否存在点P,使得![]() 是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
【答案】(1)![]() ;(2)存在,理由见解析,P的坐标是
;(2)存在,理由见解析,P的坐标是![]() 或
或![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)将点A和点C的坐标代入抛物线的解析式可求得b、c的值,然后令y=0可求得点B的坐标;
(2)分别过点C和点A作AC的垂线,将抛物线与P1,P2两点先求得AC的解析式,然后可求得P1C和P2A的解析式,最后再求得P1C和P2A与抛物线的交点坐标即可;
(3)连接OD.先证明四边形OEDF为矩形,从而得到OD=EF,然后根据垂线段最短可求得点D的纵坐标,从而得到点P的纵坐标,然后由抛物线的解析式可求得点P的坐标.
解:(1)∵将点A和点C的坐标代入抛物线的解析式得:![]() ,解得:b=-2,c=-3.
,解得:b=-2,c=-3.
∴抛物线的解析式为y=x2-2x-3.
∵令x2-2x-3=0,解得:x1=-1,x2=3.
∴点B的坐标为(-1,0).
故答案为:-2;-3;(-1,0).
(2)存在.
理由:如图所示: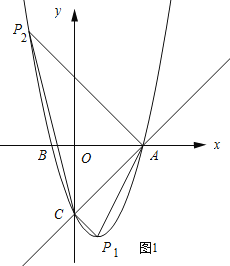
①当∠ACP1=90°.
由(1)可知点A的坐标为(3,0).
设AC的解析式为y=kx-3.
∵将点A的坐标代入得3k-3=0,解得k=1,
∴直线AC的解析式为y=x-3.
∴直线CP1的解析式为y=-x-3.
∵将y=-x-3与y=x2-2x-3联立解得x1=1,x2=0(舍去),
∴点P1的坐标为(1,-4).
②当∠P2AC=90°时.
设AP2的解析式为y=-x+b.
∵将x=3,y=0代入得:-3+b=0,解得b=3.
∴直线AP2的解析式为y=-x+3.
∵将y=-x+3与y=x2-2x-3联立解得x1=-2,x2=3(舍去),
∴点P2的坐标为(-2,5).
综上所述,P的坐标是(1,-4)或(-2,5).
(3)如图2所示:连接OD.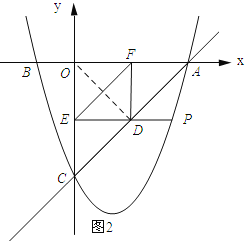
由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短.
由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC,
∴D是AC的中点.
又∵DF∥OC,
∴DF=![]() .
.
∴点P的纵坐标是![]() .
.
∴x22x3=![]() ,解得:x=
,解得:x=![]() .
.
∴当EF最短时,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 文敬图书课时先锋系列答案
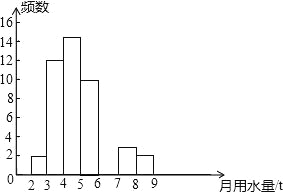
文敬图书课时先锋系列答案【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | a | b |
5≤x<6 | 10 | 20% |
6≤x<7 | c | 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)频数分布表中a= ,b= .(填百分比),c= ;补全频数分布直方图.
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有 户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.