题目内容
(本小题满分12分)已知抛物线C的方程C:y 2 ="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于
 ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
(I)抛物线C的方程为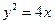 ,其准线方程为
,其准线方程为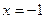 (II)符合题意的直线l 存在,其方程为2x+y-1 =0.解析:
(II)符合题意的直线l 存在,其方程为2x+y-1 =0.解析:
本小题主要考查直线、抛物线等基础知识,考查推理论证能力、运算求解能力,考查函数方程思想、数形结合思想、化归与转化思想、分类与整合思想.满分12分.
解:(Ⅰ)将(1,-2)代入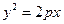 ,所以
,所以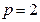 .
.
故所求的抛物线C的方程为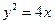 ,其准线方程为
,其准线方程为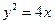
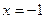 .
.
(Ⅱ)假设存在符合题意的直线l ,其方程为y=-2x + t ,
由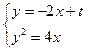 ,得y2 +2 y -2 t=0.
,得y2 +2 y -2 t=0.
因为直线l与抛物线C有公共点,所以得Δ="4+8" t,解得t ≥-1/2 .
另一方面,由直线OA与l的距离d=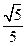 ,可得
,可得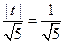 ,解得t=±1.
,解得t=±1.
因为-1∉[-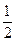 ,+∞),1∈[-
,+∞),1∈[-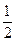 ,+∞),所以符合题意的直线l 存在,其方程为2x+y-1 =0.
,+∞),所以符合题意的直线l 存在,其方程为2x+y-1 =0.
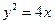 ,其准线方程为
,其准线方程为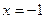 (II)符合题意的直线l 存在,其方程为2x+y-1 =0.解析:
(II)符合题意的直线l 存在,其方程为2x+y-1 =0.解析:本小题主要考查直线、抛物线等基础知识,考查推理论证能力、运算求解能力,考查函数方程思想、数形结合思想、化归与转化思想、分类与整合思想.满分12分.
解:(Ⅰ)将(1,-2)代入
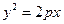 ,所以
,所以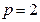 .
.故所求的抛物线C的方程为
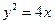 ,其准线方程为
,其准线方程为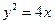
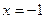 .
.(Ⅱ)假设存在符合题意的直线l ,其方程为y=-2x + t ,
由
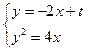 ,得y2 +2 y -2 t=0.
,得y2 +2 y -2 t=0.因为直线l与抛物线C有公共点,所以得Δ="4+8" t,解得t ≥-1/2 .
另一方面,由直线OA与l的距离d=
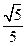 ,可得
,可得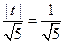 ,解得t=±1.
,解得t=±1.因为-1∉[-
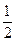 ,+∞),1∈[-
,+∞),1∈[-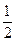 ,+∞),所以符合题意的直线l 存在,其方程为2x+y-1 =0.
,+∞),所以符合题意的直线l 存在,其方程为2x+y-1 =0. 
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:


 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线


