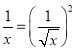题目内容
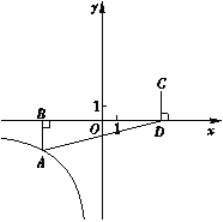
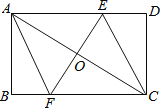
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0),(1)求抛物线的解析式_____.(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P′,当点P′落在第二象限内,P′A2取得最小值时,求m的值_____.
【答案】y=x2﹣2x﹣3 ![]()
【解析】
(1)首先把A(﹣1,0)代入y=x2+bx﹣3,得出b=﹣2,即抛物线的解析式为y=x2﹣2x﹣3;
(2)由题意可知P′(﹣m,﹣t)在第二象限,即可判定﹣m<0,﹣t>0,即m>0,t<0,因为抛物线的顶点坐标为(1,﹣4),可得出﹣4≤t<0,又根据P在抛物线上,可得出t=m2﹣2m﹣3,进而得出m2﹣2m=t+3,根据两点坐标A(﹣1,0),P′(﹣m,﹣t),即可求出P′A2=(﹣m+1)2+(﹣t)2=m2﹣2m+1+t2=t2+t+4=(t+![]() )2+
)2+![]() ;可判定当t=﹣
;可判定当t=﹣![]() 时,P′A2有最小值,即可求出m的值为
时,P′A2有最小值,即可求出m的值为![]() .
.
解:(1)把A(﹣1,0)代入y=x2+bx﹣3得:0=1﹣b﹣3,
解得:b=﹣2,
即抛物线的解析式为y=x2﹣2x﹣3,
故答案为:y=x2﹣2x﹣3;
(2)由题意可知P′(﹣m,﹣t)在第二象限,
∴﹣m<0,﹣t>0,即m>0,t<0,
∵抛物线的顶点坐标为(1,﹣4),
∴﹣4≤t<0,
∵P在抛物线上,
∴t=m2﹣2m﹣3,
∴m2﹣2m=t+3,
∵A(﹣1,0),P′(﹣m,﹣t),
∴P′A2=(﹣m+1)2+(﹣t)2=m2﹣2m+1+t2=t2+t+4=(t+![]() )2+
)2+![]() ;
;
∴当t=﹣![]() 时,P′A2有最小值,
时,P′A2有最小值,
∴﹣![]() =m2﹣2m﹣3,解得m=
=m2﹣2m﹣3,解得m=![]() 或m=
或m=![]() ,
,
∵m>0,
∴m=![]() 不合题意,舍去,
不合题意,舍去,
∴m的值为![]() ,
,
故答案为:![]()

 阅读快车系列答案
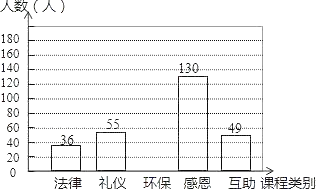
阅读快车系列答案【题目】某校有学生3600人,在“文明我先行”的活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了一些学生,并制成统计表和统计图:
课程类别 | 频数 | 频率 |
法律 | 36 | 0.09 |
礼仪 | 55 | 0.1375 |
环保 | m | a |
感恩 | 130 | 0.325 |
互助 | 49 | 0.1225 |
合计 | n | 1.00 |
(1)在这次调查活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”)a= ,m= ,n= .
(2)请补全条形统计图,如果要画一个“校本课程报名意向扇形统计图”,那么“环保”类校本课程所对应的扇形圆心角应为 度;
(3)请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人?