Question

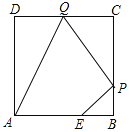
【题目】如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），则四边形AEPQ的周长的最小值是 ．

Answer 1

【答案】．

【解析】

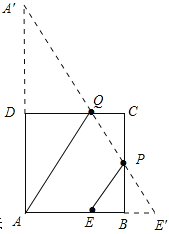
试题解析：如图所示

，

作E关于BC的对称点E′，点A关于DC的对称点A′，连接A′E′，四边形AEPQ的周长最小，

∵AD=A′D=3，BE=BE′=1，

∴AA′=6，AE′=4．

∵DQ∥AE′，D是AA′的中点，

∴DQ是△AA′E′的中位线，

∴DQ=AE′=2；CQ=DC-CQ=3-2=1，

∵BP∥AA′，

∴△BE′P∽△AE′A′，

∴，即，BP=，CP=BC-BP=3-=，

S四边形AEPQ=S正方形ABCD-S△ADQ-S△PCQ-SBEP=9-ADDQ-CQCP-BEBP

=9-×3×2-×1×-×1×=．