Question

观察下面的一系列等式， 32－12＝8×1
52－32＝8×2
72－52＝8×3
92－72＝8×4……
则第n个等式为        ，计算20012－19992=      ．

Answer 1

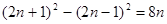
从式子的左边分析，2个连续奇数的平方，大奇数的平方减去小的平方；从等式右边知道变化数n是自然数，8是不变数，进而得出答案．
解答：解：∵3²-1²=8×1；5²-3²=8×2；7²-5²=8×3；9²-7²=8×4；…
∴第n个等式为：（2n+1）²-（2n-1）²=8n．
故答案为：（2n+1）²-（2n-1）²=8n．