题目内容
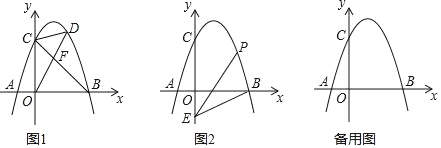
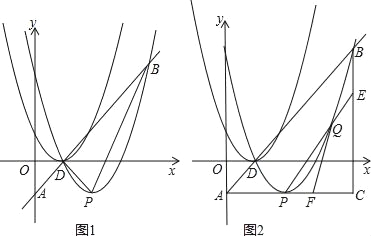
【题目】如图1,抛物线C1:y=ax2+bx+1的顶点坐标为D(1,0)且经过点(0,1),将抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,直线y=x+c,经过点D交y轴于点A,交抛物线C2于点B,抛物线C2的顶点为P.
(1)求抛物线C1的解析式;
(2)如图2,连结AP,过点B作BC⊥AP交AP的延长线于C,设点Q为抛物线上点P至点B之间的一动点,连结BQ并延长交AC于点F,
①当点Q运动到什么位置时,S△PBD×S△BCF=8?
②连接PQ并延长交BC于点E,试证明:FC(AC+EC)为定值.
【答案】(1)y=x2﹣2x+1;(2)点Q运动到x轴时,S△PBD×S△BCF=8;②证明见解析.
【解析】
(1)已知顶点D的坐标,设抛物线的顶点式为:y=a(x-1)2,将点(0,1)代入即可;
(2)根据平移规律求出平移后抛物线的顶点坐标,即P(2,-1),根据顶点式,得平移后抛物线解析式y=(x-2)2-1,由解析式,得A(0,-1),B(4,3),可求△DBP的面积;
(3)由QM∥CE,得△PQM∽△PEC,利用相似比求EC,由QN∥FC,得△BQN∽△BFC,利用相似比求FC,已知AC=4,再计算FC(AC+EC)为定值.
(1)把顶点坐标为D(1,0)和点(0,1)坐标代入y=ax2+bx+1,
解得:抛物线的方程为:y=x2﹣2x+1;
(2)抛物线C1向右平移1个单位,向下平移1个单位得到抛物抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,
则抛物线C2的方程为:y=(x﹣2)2﹣1=x2﹣4x+3,
此时顶点P坐标为(2,﹣1),A(0,﹣1)、B(4,3),
①则:S△PBD=3,S△BCF=![]() ,
,
设点Q(m,m2﹣4m+3),把Q、B点坐标代入一次函数表达式,
解得:BQ所在的直线方程为:y=mx+(3﹣4m),
则:F(![]() ,﹣1),S△BCF=
,﹣1),S△BCF=![]() FC(yB﹣yC)=
FC(yB﹣yC)=![]() =
=![]() ,
,
则m=3,点Q坐标为:(3,0),即:点Q运动到x轴时,S△PBD×S△BCF=8;
②如下图所示,过Q点分别作AC、BC的垂线QM、QN,

设:Q(t,t2﹣4t+3),则QM=CN=(t﹣2)2,MC=QN=4﹣t,
∵QM∥CE,∴![]() =
=![]() ,则:
,则:![]() =
=![]() ,解得:EC=2t﹣4,
,解得:EC=2t﹣4,
∵QN∥FC,![]() ,则:FC=
,则:FC=![]() ,而AC=4,
,而AC=4,
∴FC(AC+EC)=![]() (4+2t﹣4)=8,为定值.
(4+2t﹣4)=8,为定值.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.