题目内容
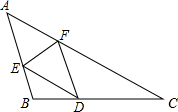 (2010•集美区模拟)如图,在△ABC中,分别在AB、AC上选取E、F两点,使得△AEF沿EF折叠后,点A的对应点D恰好落在BC上,且FD∥AB.
(2010•集美区模拟)如图,在△ABC中,分别在AB、AC上选取E、F两点,使得△AEF沿EF折叠后,点A的对应点D恰好落在BC上,且FD∥AB.(1)求证:四边形AEDF是菱形;
(2)如果AB=3,AC=6,求菱形AEDF的边长.
分析:(1)由FD∥AB,且使得△AEF沿EF折叠后,点A的对应点D恰好落在BC上,易证得△DEF是等腰三角形,即DE=DF,又由AE=DE,AF=DF,即可得AE=DE=DF=AF,即可证得四边形AEDF是菱形;
(2)易证得△CFD∽△CAB,然后由相似三角形的对应边成比例,即可求得菱形AEDF的边长.
(2)易证得△CFD∽△CAB,然后由相似三角形的对应边成比例,即可求得菱形AEDF的边长.
解答: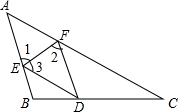 (1)证明:∵FD∥AB,
(1)证明:∵FD∥AB,
∴∠1=∠2,
由折叠的性质可得:∠1=∠3,AE=DE,AF=DF,
∴∠2=∠3,
∴DE=DF,
∵AE=DE=DF=AF,
∴四边形AEDF是菱形;
(2)∵FD∥AB,
∴△CFD∽△CAB,
∴
=
,
∵四边形AEDF是菱形,
∴FD=AF,
∵AB=3,AC=6,
∴
=
,
解得:AF=2,
故菱形AEDF的边长为2.
 (1)证明:∵FD∥AB,
(1)证明:∵FD∥AB,∴∠1=∠2,
由折叠的性质可得:∠1=∠3,AE=DE,AF=DF,
∴∠2=∠3,
∴DE=DF,
∵AE=DE=DF=AF,
∴四边形AEDF是菱形;
(2)∵FD∥AB,
∴△CFD∽△CAB,
∴
| CF |
| AC |
| FD |
| AB |
∵四边形AEDF是菱形,
∴FD=AF,
∵AB=3,AC=6,
∴
| 6-AF |
| 6 |
| AF |
| 3 |
解得:AF=2,
故菱形AEDF的边长为2.
点评:此题考查了相似三角形的判定与性质、菱形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
 (2010•集美区模拟)下列立体图形(如图)的俯视图是( )
(2010•集美区模拟)下列立体图形(如图)的俯视图是( ) (2010•集美区模拟)如图,直线y=-
(2010•集美区模拟)如图,直线y=-