题目内容
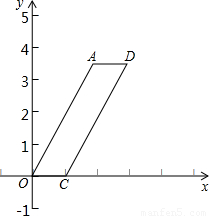
在平行四边形AOCD中,已知AO=4cm,OC=1cm,∠ADC=50°.以点O为原点,OC 为x轴,建立如图所示的直角坐标系.
为x轴,建立如图所示的直角坐标系.(1)写出平行四边形AOCD四个顶点的坐标(精确到0.1);
(2)设点F(x,0)是x右半轴上的一个动点,两直线AF、DC交于点E.
①若DE为z(cm);试求z(cm)与x(cm)之间的函数关系式,并写出x的取值范围;
②当点F运动到什么位置(用坐标表示并精确到0.1)时,△AED是等腰三角形,请说明理由.
分析:(1)已知AO=4cm,∠ADC=50°,可求出A点的横、纵坐标的值,OC=1cm,继而可求出C和D点的坐标;
(2)当点F在OC上,由△EFC∽△EAD,对应边的比相等,可列出函数关系式:若△AED是等腰三角形,分两种情况讨论.
(2)当点F在OC上,由△EFC∽△EAD,对应边的比相等,可列出函数关系式:若△AED是等腰三角形,分两种情况讨论.
解答: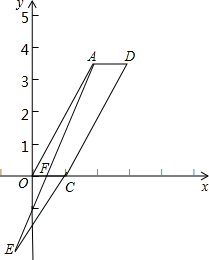 解:(1)∵AO=4cm,∠ADC=50°,
解:(1)∵AO=4cm,∠ADC=50°,
∴点A的纵坐标为sin50°×4=0.77×4=3.1,横坐标为cos50°×4=0.64×4=2.6.
又OC=1cm,
∴平行四边形AOCD四个顶点的坐标(精确到0.1)分别为:
A(2.6,3.1)、D(3.6,3.1)、C(1,0)、O(0,0).
(2)①依题意得:x>0.
当点F在OC上(如图),
由△EFC∽△EAD,得
=
,∴z=
当点F在OC的延长线上,同法可求得z=
综上,z=
(x>0)
②若AD=DE,即z=1时,由
=1,解得x=4
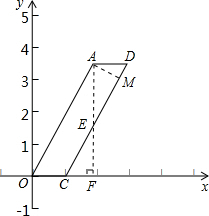
若AD=AE,过点A作AM⊥DE于M(如图).
在Rt△AMD中,MD=1•cos50°,z=2MD≈1.3
∴
=1.3,解得x≈3.1
若ED=AE,过点E作EN⊥AD于N.
在Rt△END中,可求得z≈0.78,即得x≈5.1∴当F运动到点(3.1,0)、(4,0)、(5.1,0)时,△AED是等腰三角形.
 解:(1)∵AO=4cm,∠ADC=50°,
解:(1)∵AO=4cm,∠ADC=50°,∴点A的纵坐标为sin50°×4=0.77×4=3.1,横坐标为cos50°×4=0.64×4=2.6.
又OC=1cm,
∴平行四边形AOCD四个顶点的坐标(精确到0.1)分别为:
A(2.6,3.1)、D(3.6,3.1)、C(1,0)、O(0,0).
(2)①依题意得:x>0.
当点F在OC上(如图),
由△EFC∽△EAD,得
| 1-x |
| 1 |
| z-4 |
| z |
| 4 |
| x |
当点F在OC的延长线上,同法可求得z=
| 4 |
| x |

综上,z=
| 4 |
| x |
②若AD=DE,即z=1时,由
| 4 |
| x |
若AD=AE,过点A作AM⊥DE于M(如图).
在Rt△AMD中,MD=1•cos50°,z=2MD≈1.3
∴
| 4 |
| x |
若ED=AE,过点E作EN⊥AD于N.
在Rt△END中,可求得z≈0.78,即得x≈5.1∴当F运动到点(3.1,0)、(4,0)、(5.1,0)时,△AED是等腰三角形.
点评:本题考查了相似三角形的判定与性质、等腰三角形和平行四边形的性质及解直角三角形的知识,有一定难度,注意对各部分知识的熟练掌握与灵活应用是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
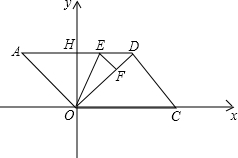 OCD=
OCD= .点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
.点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.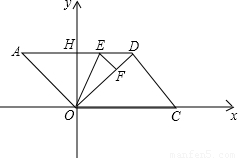
 .点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
.点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.