题目内容
【题目】如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF交于H,BF,AD的延长线交于G
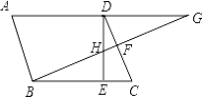
(1)求证:AB=BH
(2)若GA=10,HE=2,求AB的值
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
试题分析:(1)求出BE=DE,根据垂直推出∠CDE=∠HBE,证△BHE≌△DEC,推出BH=CD即可.
(2)根据AD∥BC推出三角形相似,得出比例式,求出BE的值,在△DEC中根据勾股定理求出CD即可.
试题解析:(1)∵DE⊥BC,BF⊥CD,
∴∠BEH=∠DEC=∠BFC=90°,
∴∠HBE+∠C=90°,∠CDE+∠C=90°,
∴∠HBE=∠CDE,
∵∠DBC=45°,∠DEB=90°,
∴∠BDE=45°=∠DBE,
∴BE=DE,
∵在△BHE和△DEC中
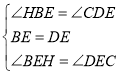 ,
,
∴△BHE≌△DEC,
∴BH=CD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AB=BH.
(2)设BE=a,则BC=AD=a+2,DE=BE=a,DH=a-2,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△DHG∽△EHB,
∴![]() ,
,
∵AG=10,
∴![]() ,
,
解得:a=4,
BE=DE=4,
在△DEC中,EC=EH=2,DE=4,由勾股定理得:CD=2![]() ,
,
∵四边形ABCD是平行四边形,
∴AB=CD=2![]() .
.

练习册系列答案
相关题目

