题目内容
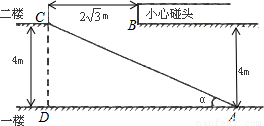
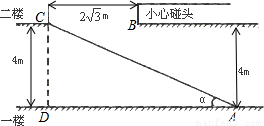
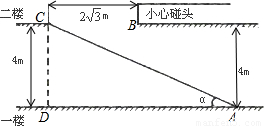
邵阳市某大型超市为方便顾客购物，准备在一至二楼之间安装电梯，如图所示，楼顶与地面平行．要使身高2米以下的人在笔直站立的情况下搭乘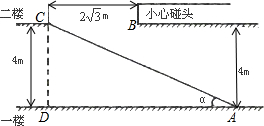
电梯时，在B处不碰到头部．请你帮该超市设计，电梯与一楼地面的夹角α最小为多少度？
分析：可过点B作BE⊥AD交AD于E，交AC于F，那么要使2米以下的人不碰头，BF的最小值就应该是2米，有CD的高是4米，我们就能求出EF的长，可通过平行线分线段成比例来得出AE，AD，EF，CD这四条边的比例关系，其中CD，EF的值都已得出，AD=AE+DE，而DE正好和BC相等，那么可在这个比例关系式中求出AE的长，那么就能在直角三角形AEF中用正切函数求出α的度数．
解答：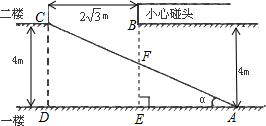
解：如图，过点B作BE⊥AD交AD于E，交AC于F．
依题意有：BF=2，DE=BC=2
．
∴CD=4，∴EF=2．
又
=
，
∴
=
．
∴AE=2
．
在Rt△AEF中，tanα=
=
=
．
∴∠α=30°．
答：电梯与一楼地面的夹角α最小为30度．
解：如图，过点B作BE⊥AD交AD于E，交AC于F．依题意有：BF=2，DE=BC=2
| 3 |
∴CD=4，∴EF=2．
又
| EF |
| CD |
| AE |
| AD |
∴
| 2 |
| 4 |
| AE | ||
AE+2
|
∴AE=2
| 3 |
在Rt△AEF中，tanα=
| EF |
| AE |
| 2 | ||
2
|
| ||
| 3 |
∴∠α=30°．
答：电梯与一楼地面的夹角α最小为30度．
点评：解此类坡度角问题，一般都是在直角三角形内进行求解．没有直角三角形的要根据已知条件来构建直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
