题目内容
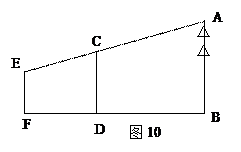
 如图,一棵树AB的顶端A的影子落在教学楼前的坪地C处,小明分别测得坪地、台阶和地面上的三段影长CE=1m,DE=2m,BD=8m,DE与地面的夹角α=30°.在同一时刻,已知一根1m长的直立竹竿在地面上的影长恰好为2m,请你帮助小明根据以上数据求出树AB的高.(结果精确到0.1m,参考数据:
如图,一棵树AB的顶端A的影子落在教学楼前的坪地C处,小明分别测得坪地、台阶和地面上的三段影长CE=1m,DE=2m,BD=8m,DE与地面的夹角α=30°.在同一时刻,已知一根1m长的直立竹竿在地面上的影长恰好为2m,请你帮助小明根据以上数据求出树AB的高.(结果精确到0.1m,参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
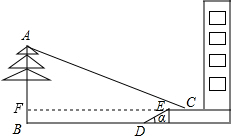 解:如图,延长CE交AB于F,
解:如图,延长CE交AB于F,∵α=30°,DE=2m,BD=8m,
∴EF=BD+DEcos30°=8+2×
 =8+
=8+ m,
m,点E到底面的距离=DEsin30°=2×
 =1m,
=1m,即BF=1m,
∴CF=EF+CE=8+
 +1=9+
+1=9+ ,
,根据同时同地物高与影长成正比得,
 =
= ,
,∴AF=
 CF=
CF= (9+
(9+ )=
)= ×10.73≈5.4m,
×10.73≈5.4m,∴树AB的高为5.4+1=6.4m.
分析:延长CE交AB于F,解直角三角形求出EF的长,点E到底面的距离,即BF的长,然后求出CF,再根据同时同地物高与影长成正比列式求出AF的长,即可得解.
点评:本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比的性质,作辅助线,把AB的长度分两段求解是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
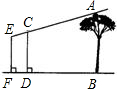 如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2米的标杆,现测量者从E处可以看到杆顶C与树顶A在同一直线上,如果测得BD=20米,FD=4米,EF=1.8米,则树的高度为
如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2米的标杆,现测量者从E处可以看到杆顶C与树顶A在同一直线上,如果测得BD=20米,FD=4米,EF=1.8米,则树的高度为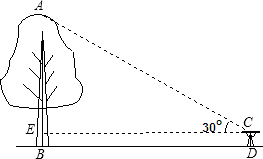 如图,我市某校初三(一)班的同学要测一棵树AB的高度.在离树24m的D处,用测角仪测得树顶A的仰角为30°,已知测角仪的高CD=1m,求树高AB(结果保留根号)
如图,我市某校初三(一)班的同学要测一棵树AB的高度.在离树24m的D处,用测角仪测得树顶A的仰角为30°,已知测角仪的高CD=1m,求树高AB(结果保留根号)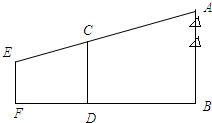
 如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2m的标杆,现测量者从E处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,则树AB的高度为
如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2m的标杆,现测量者从E处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,则树AB的高度为