题目内容
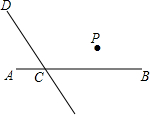 如图,直线CD与直线AB相交于点C,根据下列语句画图、解答.
如图,直线CD与直线AB相交于点C,根据下列语句画图、解答.(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,交AB于点O,垂足于CD为R;
(3)若∠DCB=120°,猜想∠POC是多少度?并说明理由.
分析:(1)过点P作∠PQA=∠DCA,交AB于点Q;
(2)过点P作∠QPR=90°,PR交AB于点O,与CD交于点R;
(3)先利用两直线平行,同旁内角互补求出∠PQC=60°,再根据PQ∥CD,PR⊥CD,得出∠QPO=90°,然后根据三角形的外角的性质得到∠POC=∠PQO+∠QPO=150°.
(2)过点P作∠QPR=90°,PR交AB于点O,与CD交于点R;
(3)先利用两直线平行,同旁内角互补求出∠PQC=60°,再根据PQ∥CD,PR⊥CD,得出∠QPO=90°,然后根据三角形的外角的性质得到∠POC=∠PQO+∠QPO=150°.
解答: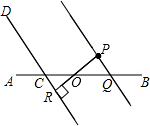 解:(1)(2)如图所示;
解:(1)(2)如图所示;
(3)∠POC=150°,理由如下:
∵PQ∥CD,
∴∠DCB+∠PQC=180°,
∵∠DCB=120°,
∴∠PQC=180°-120°=60°.
∵PQ∥CD,PR⊥CD,
∴PR⊥PQ,∠QPO=90°,
∴∠POC=∠PQO+∠QPO=60°+90°=150°.
 解:(1)(2)如图所示;
解:(1)(2)如图所示;(3)∠POC=150°,理由如下:
∵PQ∥CD,
∴∠DCB+∠PQC=180°,
∵∠DCB=120°,
∴∠PQC=180°-120°=60°.
∵PQ∥CD,PR⊥CD,
∴PR⊥PQ,∠QPO=90°,
∴∠POC=∠PQO+∠QPO=60°+90°=150°.
点评:本题考查了基本作图--平行线和垂线的画法,同时考查了平行线的性质,垂直的定义及三角形外角的性质等知识.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 37、读句画图:如图,直线CD与直线AB相交于C,
37、读句画图:如图,直线CD与直线AB相交于C, 19、读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:
19、读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:
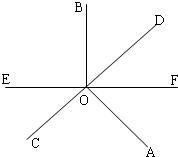 19、如图,直线CD与直线EF相交于点O,OB、OA为射线,∠BOE=∠AOD=90°,∠EOD>∠EOC,则∠DOF的补角是
19、如图,直线CD与直线EF相交于点O,OB、OA为射线,∠BOE=∠AOD=90°,∠EOD>∠EOC,则∠DOF的补角是