题目内容
(1)梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是S1、S2、S3,且S1+S3=4S2,如果AB=2010,那么则CD=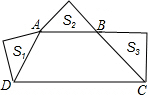
(2)已知a,b是正整数,且满足2 (
|
|
分析:(1)作BE∥AD于E,则四边形ABED是平行四边形,得∠BEC=∠ADC,DE=AB=2010,则∠EBC=90°.要求CD的长,只需根据勾股定理求得CE的长.结合等腰直角三角形的面积公式和S1+S3=4S2,即可求解;
(2)根据题意,只需保证
+
=2或
或
即可.
(2)根据题意,只需保证
|
|
| 1 |
| 2 |
| 3 |
| 2 |
解答: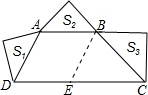 解:(1)作BE∥AD于E,则四边形ABED是平行四边形.
解:(1)作BE∥AD于E,则四边形ABED是平行四边形.
∴∠BEC=∠ADC,DE=AB=2010.
又∠ADC+∠BCD=90°,
∴∠EBC=90°.
∵S1+S3=4S2,S2=
×
×2010×2010,
∴BE2+BC2=4(S1+S3)=2010×2010×4,
∴CE=4020.
∴CD=6030.
(2)(15,15)、(60、60)、(15,60)、(60,15)、(240,240)、(135,540)、(540,135).
 解:(1)作BE∥AD于E,则四边形ABED是平行四边形.
解:(1)作BE∥AD于E,则四边形ABED是平行四边形.∴∠BEC=∠ADC,DE=AB=2010.
又∠ADC+∠BCD=90°,
∴∠EBC=90°.
∵S1+S3=4S2,S2=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE2+BC2=4(S1+S3)=2010×2010×4,
∴CE=4020.
∴CD=6030.
(2)(15,15)、(60、60)、(15,60)、(60,15)、(240,240)、(135,540)、(540,135).
点评:(1)综合运用了平行四边形的判定及性质、勾股定理以及等腰直角三角形的性质.
注意:根据等腰直角三角形斜边上的高也是斜边上的中线,斜边上的中线等于斜边的一半,知等腰直角三角形的面积等于斜边的平方的一半.
(2)考查了二次根式的化简.
注意:根据等腰直角三角形斜边上的高也是斜边上的中线,斜边上的中线等于斜边的一半,知等腰直角三角形的面积等于斜边的平方的一半.
(2)考查了二次根式的化简.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
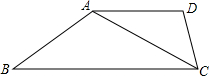 如图,在梯形ABCD中,AD∥BC,∠B=∠ACD
如图,在梯形ABCD中,AD∥BC,∠B=∠ACD