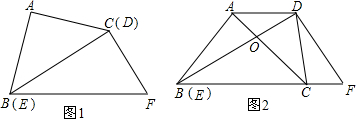题目内容
将一副直角三角板DEF按如图1摆放,使直角顶点D落在等腰Rt△ABC的斜边BC的中点上,DF,DE分别与AB,AC交于点M,N;
(1)如果把图1中的△DCN绕点D顺时方向旋转180°,得到图2,在不添加任何辅助线的情况下,图2中除△DCN≌△DBG外,你还能找到一对全等的三角形吗?写出你的结论并说明理由;
(2)将三角板DEF绕点D旋转,①当M,N分别在AB,AC上时,线段BM,CN,MN之间有一个确定的等量关系.请你写出这个关系式(不需证明);
②如图3,当点M,N分别在BA,AC的延长线上时,①的关系式是否仍然成立?写出你的结论,并说明理由.



(1)解:答案不唯一,如△MGD≌△MND;
证明:∵△DCN绕点D顺时方向旋转180°得到△DBG,
∴△DCN≌△DBG,G、D、N三点共线,
∴DN=DG,
在△MGD和△MND中,
MD=MD,∠MDG=∠MDN=90°,DN=DG,
∴△MGD≌△MND(SAS).
(2)解:①BM2+CN2=MN2;
②:①的关系式仍然成立;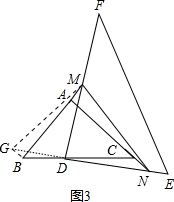
将△DCN绕点D顺时方向旋转180°,连接GM,
∴△DCN≌△DBG,
∴∠DCN=∠DBG,
∵△ABC为等腰直角三角形,
∴∠ABC=∠ACD=45°,
∴∠DCN=∠DBG=135°,
∠ABG=∠DBG-∠ABC=90°,
同理可证△MGD≌△MND,
∴GM=MN,
在Rt△GBM中:BG2+BM2=GM2,
∴BM2+CN2=MN2.
分析:(1)应找较简单的,易得到结论的两个三角形,比如△MGD≌△MND,可利用边角边证其全等;
(2)①应利用题中已知的,和(1)中求得的两个三角形全等,得到CN=BG,MN=MG,易得∠MBG=∠ABD+∠CBG=90°,那么可得所求三边的关系;
②按照前面的方法构造同样的三角形全等把所求的三条线段进行转移,方法同①.
点评:此题把旋转的性质、全等三角形的判定和勾股定理结合求解.综合性强,难度大.考查了学生综合运用数学知识的能力.注意找全等应找容易求得全等的三角形,应用类比的方法求解复杂问题.
证明:∵△DCN绕点D顺时方向旋转180°得到△DBG,
∴△DCN≌△DBG,G、D、N三点共线,
∴DN=DG,
在△MGD和△MND中,
MD=MD,∠MDG=∠MDN=90°,DN=DG,
∴△MGD≌△MND(SAS).
(2)解:①BM2+CN2=MN2;
②:①的关系式仍然成立;

将△DCN绕点D顺时方向旋转180°,连接GM,
∴△DCN≌△DBG,
∴∠DCN=∠DBG,
∵△ABC为等腰直角三角形,
∴∠ABC=∠ACD=45°,
∴∠DCN=∠DBG=135°,
∠ABG=∠DBG-∠ABC=90°,
同理可证△MGD≌△MND,
∴GM=MN,
在Rt△GBM中:BG2+BM2=GM2,
∴BM2+CN2=MN2.
分析:(1)应找较简单的,易得到结论的两个三角形,比如△MGD≌△MND,可利用边角边证其全等;
(2)①应利用题中已知的,和(1)中求得的两个三角形全等,得到CN=BG,MN=MG,易得∠MBG=∠ABD+∠CBG=90°,那么可得所求三边的关系;
②按照前面的方法构造同样的三角形全等把所求的三条线段进行转移,方法同①.
点评:此题把旋转的性质、全等三角形的判定和勾股定理结合求解.综合性强,难度大.考查了学生综合运用数学知识的能力.注意找全等应找容易求得全等的三角形,应用类比的方法求解复杂问题.

练习册系列答案
相关题目



 (2012•鄂州)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长.
(2012•鄂州)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长.