题目内容
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走6米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，那么大树CD的高度约为（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）（ ）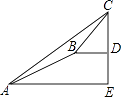
A.8.1米
B.17.2米
C.19.7米
D.25.5米
【答案】A
【解析】解：作BF⊥AE于F，如图所示：
则FE=BD=6米，DE=BF，
∵斜面AB的坡度i=1：2.4，
∴AF=2.4BF，
设BF=x米，则AF=2.4x米，
在Rt△ABF中，由勾股定理得：x2+（2.4x）2=132，
解得：x=5，
∴DE=BF=5米，AF=12米，
∴AE=AF+FE=18米，
在Rt△ACE中，CE=AEtan36°=18×0.73=13.14米，
∴CD=CE﹣DE=13.14米﹣5米≈8.1米；
故答案为：A．
通过作垂线构造直角三角形把已知角放到直角三角形中，利用三角函数和勾股定理，求出CE、DE，作差可得CD.
练习册系列答案
相关题目
【题目】下表是橘子的销售额随橘子卖出质量的变化表：
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
（1）这个表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）当橘子卖出5千克时，销售额是_______元.
（3）如果用
表示橘子卖出的质量，
表示销售额，按表中给出的关系，与之间的关系式为______.
（4）当橘子的销售额是100元时，共卖出多少千克橘子？