题目内容
【题目】如图,OE,OF分别是△ABC中AB,AC边的中垂线(即垂直平分线),∠OBC,∠OCB的平分线相交于点I,试判断OI与BC的位置关系,并给出证明.
【答案】解:OI⊥BC.理由如下 :
证明:如图,连接AO,延长OI交BC于点M.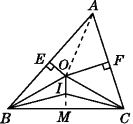
∵OE,OF分别为AB,AC的中垂线,∴OA=OB,OA=OC.∴OB=OC.
又∵BI,CI分别为∠OBC,∠OCB的平分线,∴点I必在∠BOC的平分线上.
∴∠BOI=∠COI.
∵OE,OF分别是△ABC中AB,AC边的中垂线 ,
∴OA=OB,OA=OC;
∴ OB=OC
在△BOM和△COM中,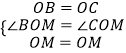
∴△BOM≌△COM(SAS).
∴∠BMO=∠CMO.
又∵∠BMO+∠CMO=180°,
∴∠BMO=∠CMO=90°,
∴OI⊥BC.
【解析】OI⊥BC.理由如下 :如图,连接AO,延长OI交BC于点M.根据角平分线的性质得出点I必在∠BOC的平分线上,根据角平分线的定义得出∠BOI=∠COI.根据中垂线的性质得出OA=OB,OA=OC;根据等量代换得出 OB=OC,从而利用SAS判断出△BOM≌△COM,根据全等三角形对应角相等得出∠BMO=∠CMO.根据平角的定义得出∠BMO+∠CMO=180°,从而得出∠BMO=∠CMO=90°,即OI⊥BC 。
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角平分线的性质定理的理解,了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目
